
Calculus, Comparison Test (LCT), 11 4 #7
Calculus, Algebra and more at www.blackpenredpen.com Differential equation, factoring, linear equation, quadratic equation, derivatives, integrals, stewart calculus 7th edition, algebra.
From playlist Calculus, Sect 11.4, Direct & Limit Comparison Test

3_5_3 The Integral Test and Comaprison Tests
The integral test for convergence of a series
From playlist Advanced Calculus / Multivariable Calculus

Math 139 Fourier Analysis Lecture 28: Finite Fourier Analysis
Background knowledge: abelian group; congruence mod N; equivalence relation; Z/NZ; group isomorphism with Z(N), the group of Nth roots of unity. Inner product space of functions on Z(N); orthonormal basis (characters); Fourier coefficients.
From playlist Course 8: Fourier Analysis

The true second derivative test
In this video I present the second derivative test in multivariable calculus, which is used to find local maxima/minima/saddle points of a function. However, unlike the nonsense they usually teach in the books, here I'm presenting a more elegant way with some linear algebra blended in. I'm
From playlist Partial Derivatives

Determining if a vector is a linear combination of other vectors
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Determining if a vector is a linear combination of other vectors
From playlist Linear Algebra

Numerical Homogenization by Localized Orthogonal Decomposition (Lecture 2) by Daniel Peterseim
DISCUSSION MEETING Multi-Scale Analysis: Thematic Lectures and Meeting (MATHLEC-2021, ONLINE) ORGANIZERS: Patrizia Donato (University of Rouen Normandie, France), Antonio Gaudiello (Università degli Studi di Napoli Federico II, Italy), Editha Jose (University of the Philippines Los Baño
From playlist Multi-scale Analysis: Thematic Lectures And Meeting (MATHLEC-2021) (ONLINE)

Lec 20 | MIT Finite Element Procedures for Solids and Structures, Nonlinear Analysis
Lecture 20: Beam, plate, and shell elements II Instructor: Klaus-Jürgen Bathe View the complete course: http://ocw.mit.edu/RES2-002S10 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT Nonlinear Finite Element Analysis
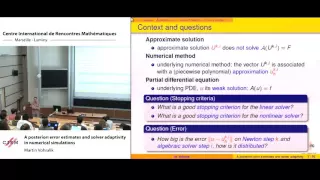
Martin Vohralik: A posteriori error estimates and solver adaptivity in numerical simulations
Abstract: We review how to bound the error between the unknown weak solution of a PDE and its numerical approximation via a fully computable a posteriori estimate. We focus on approximations obtained at an arbitrary step of a linearization (Newton-Raphson, fixed point, ...) and algebraic s
From playlist Numerical Analysis and Scientific Computing

Marta D'Elia: A coupling strategy for nonlocal and local models with applications ...
The use of nonlocal models in science and engineering applications has been steadily increasing over the past decade. The ability of nonlocal theories to accurately capture effects that are difficult or impossible to represent by local Partial Differential Equation (PDE) models motivates a
From playlist HIM Lectures: Trimester Program "Multiscale Problems"

Guanglian Li: Error analysis of a variational multiscale stabilization for convection-
Guanglian Li: Error analysis of a variational multiscale stabilization for convection-dominated diffusion equations in 2d The lecture was held within the framework of the Hausdorff Trimester Program Multiscale Problems: Workshop on Non-local Material Models and Concurrent Multiscale Metho
From playlist HIM Lectures: Trimester Program "Multiscale Problems"

Axel Målqvist: Localization of multiscale problems
The lecture was held within the framework of the Hausdorff Trimester Program Multiscale Problems: Workshop on Numerical Inverse and Stochastic Homogenization. (13.02.2017) We will present the Local Orthogonal Decomposition technique for solving partial differential equations with multisca
From playlist HIM Lectures: Trimester Program "Multiscale Problems"

3_5_1 The Integral Test and Comparison Tests
The integral test for convergence of a series.
From playlist Advanced Calculus / Multivariable Calculus

Moduli Stacks of Galois Representations by Mathew Emerton
Program Recent developments around p-adic modular forms (ONLINE) ORGANIZERS: Debargha Banerjee (IISER Pune, India) and Denis Benois (University of Bordeaux, France) DATE: 30 November 2020 to 04 December 2020 VENUE: Online This is a follow up of the conference organized last year arou
From playlist Recent Developments Around P-adic Modular Forms (Online)

Infinite Limits With Equal Exponents (Calculus)
#Calculus #Math #Engineering #tiktok #NicholasGKK #shorts
From playlist Calculus

Math 139 Fourier Analysis Lecture 32: Fourier Analysis on Finite Abelian Groups
Proving that the dual group has the same order as the group (to show the characters form an orthonormal basis for the functions on the group). Fourier analysis on finite abelian groups: Fourier coefficients; Fourier series; Fourier inversion formula; Plancherel/Parseval theorem. Statemen
From playlist Course 8: Fourier Analysis

Dynamics on character varieties - William Goldman
Character Varieties, Dynamics and Arithmetic Topic: Dynamics on character varieties Speaker: William Goldman Affiliation: University of Maryland; Member, School of Mathematics Date: November 10, 2021 In these two talks, I will describe how the classification of locally homogeneous geomet
From playlist Mathematics

3_5_4 The Integral Test and Comparison Tests
The limit comparison test.
From playlist Advanced Calculus / Multivariable Calculus

Numerical Homogenization by Localized Orthogonal Decomposition (Lecture 3) by Daniel Peterseim
DISCUSSION MEETING Multi-Scale Analysis: Thematic Lectures and Meeting (MATHLEC-2021, ONLINE) ORGANIZERS: Patrizia Donato (University of Rouen Normandie, France), Antonio Gaudiello (Università degli Studi di Napoli Federico II, Italy), Editha Jose (University of the Philippines Los Baño
From playlist Multi-scale Analysis: Thematic Lectures And Meeting (MATHLEC-2021) (ONLINE)

3_5_2 The Integral Test and Comparison Tests
The integral test for convergence of a series.
From playlist Advanced Calculus / Multivariable Calculus

Tired with Phase Transitions - Alessandro Treves
2015 Joshua Lederberg - John von Neumann Symposium "Towards Quantitative Biology" Alessandro Treves International School for Advanced Studies, Trieste December 2, 2015 https://www.sns.ias.edu/scsb/lederberg-vonneumann2015 More videos on http://video.ias.edu
From playlist Joshua Lederberg - John von Neumann Symposium