
What is the definition of a parabola
Learn all about parabolas in conic sections. We will discover the basic definitions such as the vertex, focus, directrix, and axis of symmetry. We will also take a look a basic processes such as graphing, writing the equation and identifying a parabolas parts when given an equation in sta
From playlist Learn all about Parabolas #Conics
Introduction to Parametric Equations
This video defines a parametric equations and shows how to graph a parametric equation by hand. http://mathispower4u.yolasite.com/
From playlist Parametric Equations
Linearly Parametrized Curves | Algebraic Calculus One | Wild Egg
Parametrized curves figure prominently in the Algebraic Calculus, and they coincide with de Casteljau Bezier curves. The simplest case are the linearly parametrized curves given by a pair of linear polynomials of polynumbers. This gives us an alternate view of oriented polygonal splines.
From playlist Algebraic Calculus One

Mechanical Engineering: Forces on Submerged Surfaces (8 of 15) x=? of Dam Sections***
Visit http://ilectureonline.com for more math and science lectures! In this video I find the distances to the centroids of a parabolic dam sections of to the distributed load of the water on the dam. Next video in this series can be seen at:
From playlist MECHANICAL ENGINEERING 6 FORCES ON SUBMERGED SURFACES

Parametrizing Curves in the Complex Plane 2
Complex Analysis: We give a recipe for parametrizing curves in the complex plane. In this part, we parametrize circles and semicircles.
From playlist Complex Analysis
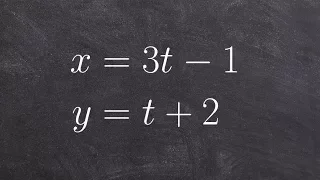
How to eliminate the parameter to identify the linear equation
Learn how to eliminate the parameter in a parametric equation. A parametric equation is a set of equations that express a set of quantities as explicit functions of a number of independent variables, known as parameters. Eliminating the parameter allows us to write parametric equation in r
From playlist Parametric Equations
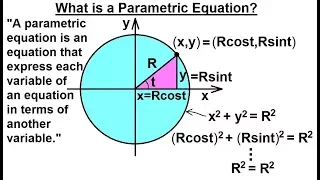
Calculus 2: Parametric Equations (1 of 20) What is a Parametric Equation?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is a parametric equation. A parametric equation is an equation that expresses each variable of an equation in terms of another variable. Next video in the series can be seen at: https://
From playlist CALCULUS 2 CH 17 PARAMETRIC EQUATIONS

Parametric Surfaces In this video, I give 5 examples of how to parametrize surfaces. This is similar to parametrizing a curve, except that this time you need two variables. This is an important tool for surface integrals, which is a way of integrating a function on a surface. Parametriza
From playlist Vector Calculus

Parametric equations on one Cartesian path (1 of 2: Introduction)
More resources available at www.misterwootube.com
From playlist Mathematical Exploration

algebraic geometry 22 Toric varieties
This lecture is part of an online algebraic geometry course, based on chapter I of "Algebraic geometry" by Hartshorne. It describes toric varieties as examples of abstract varieties. For more about these see the book "Introduction to toric varieties" by Fulton.
From playlist Algebraic geometry I: Varieties

Nick Edelen: Degeneration of 7-dimensional minimal hypersurfaces with bounded index
Abstract: A 7D minimal and locally-stable hypersurface will in general have a discrete singular set, provided it has no singularities modeled on a union of half-planes. We show in this talk that the geometry/topology/singular set of these surfaces has uniform control, in the following sens
From playlist MATRIX-SMRI Symposium: Singularities in Geometric Flows
To learn more about Wolfram Technology Conference, please visit: https://www.wolfram.com/events/technology-conference/ Speaker: Rob Knapp Wolfram developers and colleagues discussed the latest in innovative technologies for cloud computing, interactive deployment, mobile devices, and mor
From playlist Wolfram Technology Conference 2017

NOSE CONES in Kerbal Space Program - Do you need them?
Patreon page: https://www.patreon.com/user?u=2318196&ty=h Hello and welcome to What Da Math! In this video, we will discover if nose cones are needed and which ones you should use in Kerbal Space Program. Part 1 of the investigation is here: https://www.youtube.com/watch?v=4n6gkvUoG4o
From playlist Kerbal Space Program and Math

MIT 6.849 Geometric Folding Algorithms: Linkages, Origami, Polyhedra, Fall 2012 View the complete course: http://ocw.mit.edu/6-849F12 Instructor: Erik Demaine This lecture focuses on the folding of the backbone chain of proteins in relation to fixed-angle linkages. Four problems types (sp
From playlist MIT 6.849 Geometric Folding Algorithms, Fall 2012

Volume of a Frustum | Grade 7-9 Series | GCSE Maths Tutor
A video revising the techniques and strategies for working out the volume of a frustum (Higher Only). This video is part of the Geometry module in GCSE maths, see my other videos below to continue with the series. Don’t forget to check these videos out: Part 1 - The Entire GCSE in Only
From playlist Geometry

Lecture 2 | Convex Optimization I (Stanford)
Guest Lecturer Jacob Mattingley covers convex sets and their applications in electrical engineering and beyond for the course, Convex Optimization I (EE 364A). Convex Optimization I concentrates on recognizing and solving convex optimization problems that arise in engineering. Convex se
From playlist Lecture Collection | Convex Optimization

Jeff CHEEGER - Noncollapsed Gromov - Hausdorff limit spaces with Ricci curvature bounded below
Abstract: https://indico.math.cnrs.fr/event/2432/material/17/0.pdf
From playlist Riemannian Geometry Past, Present and Future: an homage to Marcel Berger

Parametrizing circles | Arithmetic and Geometry Math Foundations 29 | N J Wildberger
How to describe all the points on a circle, using a rational parametrization. This is a major improvement on the usual transcendental parametrization with circular functions. Also some interesting number theory arises when we ask which lines through the center of a circle meet that circle
From playlist Math Foundations

