Parabolic fractal distribution

Discrete distributions

In probability and statistics, the parabolic fractal distribution is a type of discrete probability distribution in which the logarithm of the frequency or size of entities in a population is a quadratic polynomial of the logarithm of the rank (with the largest example having rank 1). This can markedly improve the fit over a simple power-law relationship (see references below). In the Laherrère/Deheuvels paper below, examples include galaxy sizes (ordered by luminosity), towns (in the USA, France, and world), spoken languages (by number of speakers) in the world, and oil fields in the world (by size). They also mention utility for this distribution in fitting seismic events (no example). The authors assert the advantage of this distribution is that it can be fitted using the largest known examples of the population being modeled, which are often readily available and complete, then the fitted parameters found can be used to compute the size of the entire population. So, for example, the populations of the hundred largest cities on the planet can be sorted and fitted, and the parameters found used to extrapolate to the smallest villages, to estimate the population of the planet. Another example is estimating total world oil reserves using the largest fields. In a number of applications, there is a so-called King effect where the top-ranked item(s) have a significantly greater frequency or size than the model predicts on the basis of the other items. The Laherrère/Deheuvels paper shows the example of Paris, when sorting the sizes of towns in France. When the paper was written Paris was the largest city with about ten million inhabitants, but the next largest town had only about 1.5 million. Towns in France excluding Paris closely follow a parabolic distribution, well enough that the 56 largest gave a very good estimate of the population of the country. But that distribution would predict the largest city to have about two million inhabitants, not 10 million. The King Effect is named after the notion that a King must defeat all rivals for the throne and takes their wealth, estates and power, thereby creating a buffer between himself and the next-richest of his subjects. That specific effect (intentionally created) may apply to corporate sizes, where the largest businesses use their wealth to buy up smaller rivals. Absent intent, the King Effect may occur as a result of some persistent growth advantage due to scale, or to some unique advantage. Larger cities are more efficient connectors of people, talent and other resources. Unique advantages might include being a port city, or a Capital city where law is made, or a center of activity where physical proximity increases opportunity and creates a feedback loop. An example is the motion picture industry; where actors, writers and other workers move to where the most studios are, and new studios are founded in the same place because that is where the most talent resides. To test for the King Effect, the distribution must be fitted excluding the 'k' top-ranked items, but without assigning new rank numbers to the remaining members of the population. For example, in France the ranks are (as of 2010): 1. * Paris, 12.09M 2. * Lyon, 2.12M 3. * Marseille, 1.72M 4. * Toulouse, 1.20M 5. * Lille, 1.15M A fitting algorithm would process pairs {(1,12.09), (2,2.12), (3,1.72), (4,1.20), (5,1.15)} and find the parameters for the best parabolic fit through those points. To test for the King Effect we just exclude the first pair (or first 'k' pairs), and find parabolic parameters that fit the remainder of the points. So for France we wouldfit the four points {(2,2.12), (3,1.72), (4,1.20), (5,1.15)}. Then we can use those parameters to estimate the size of cities ranked [1,k] and determine if they are King Effect members or normal members. By comparison, Zipf's law fits a line through the points (also using the log of the rank and log of the value). A parabola (with one more parameter) will fit better, but far from the vertex the parabola is also nearly linear. Thus, although it is a judgment call for the statistician, if the fitted parameters put the vertex far from the points fitted, or if the parabolic curve is not a significantly better fit than a line, those may be symptomatic of overfitting (aka over-parameterization). The line (with two parameters instead of three) is probably the better generalization. More parameters always fit better, but at the cost of adding unexplained parameters or unwarranted assumptions (such as the assumption that a slight parabolic curve is a more appropriate model than a line). Alternatively, it is possible to force the fitted parabola to have its vertex at the rank 1 position. In that case, it is not certain the parabola will fit better (have less error) than a straight line; and the choice might be made between the two based on which has the least error. (Wikipedia).

Eliminating the parameter for parametric trigonometric

Learn how to eliminate the parameter in a parametric equation. A parametric equation is a set of equations that express a set of quantities as explicit functions of a number of independent variables, known as parameters. Eliminating the parameter allows us to write parametric equation in r

From playlist Parametric Equations

The Beauty of Fractal Geometry (#SoME2)

0:00 — Sierpiński carpet 0:18 — Pythagoras tree 0:37 — Pythagoras tree 2 0:50 — Unnamed fractal circles 1:12 — Dragon Curve 1:30 — Barnsley fern 1:44 — Question for you! 2:05 — Koch snowflake 2:26 — Sierpiński triangle 2:47 — Cantor set 3:03 — Hilbert curve 3:22 — Unnamed fractal squares 3

From playlist Summer of Math Exposition 2 videos

Fractals are typically not self-similar

An explanation of fractal dimension. Help fund future projects: https://www.patreon.com/3blue1brown An equally valuable form of support is to simply share some of the videos. Special thanks to these supporters: https://3b1b.co/fractals-thanks And by Affirm: https://www.affirm.com/careers H

From playlist Explainers

Rigidity on Homogeneous Bundles by Alexander Gorodnik

DISCUSSION MEETING STRUCTURED LIGHT AND SPIN-ORBIT PHOTONICS ORGANIZERS: Bimalendu Deb (IACS Kolkata, India), Tarak Nath Dey (IIT Guwahati, India), Subhasish Dutta Gupta (UOH, TIFR Hyderabad, India) and Nirmalya Ghosh (IISER Kolkata, India) DATE: 29 November 2022 to 02 December 2022 VE

From playlist Ergodic Theory and Dynamical Systems 2022

The Large-Scale Dynamics of Flows: Facts and Proofs from 1D Burgers to 3D Euler/NS by Uriel Frisch

Program Turbulence: Problems at the Interface of Mathematics and Physics (ONLINE) ORGANIZERS: Uriel Frisch (Observatoire de la Côte d'Azur and CNRS, France), Konstantin Khanin (University of Toronto, Canada) and Rahul Pandit (Indian Institute of Science, Bengaluru) DATE: 07 December 202

From playlist Turbulence: Problems at The Interface of Mathematics and Physics (Online)

Introduction to Parametric Equations

This video defines a parametric equations and shows how to graph a parametric equation by hand. http://mathispower4u.yolasite.com/

From playlist Parametric Equations

Newton Fractals

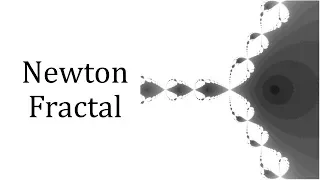
Using Newton's Method to create Fractals by plotting convergence behavior on the complex plane. Functions used in this video include arctan(z), z^3-1, sin(z), z^8-15z^4+16. Example code and images available at https://github.com/osveliz/numerical-veliz Correction: The derivative of arctan

From playlist Root Finding

Concavity and Parametric Equations Example

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Concavity and Parametric Equations Example. We find the open t-intervals on which the graph of the parametric equations is concave upward and concave downward.

From playlist Calculus

Alex Kontorovich - Diophantine problems in thin orbits

Diophantine problems in thin orbits

From playlist 28ème Journées Arithmétiques 2013

Successive Parabolic Interpolation - Jarratt's Method

Optimization method for finding extrema of functions using three points to create a parabola that is then used to find the next approximation to the solution. This lesson visualizes the behavior of the method with numeric examples as well as its convergence through fractals. Based off the

From playlist Numerical Methods

Ex 2: Find the Parametric Equations for a Lissajous Curve

This video explains how to determine possible parametric equations for a Lissajous figure. Site: http://mathispower4u.com

From playlist Parametric Equations

Davar Khoshnevisan (Utah) -- Ergodicity and CLT for SPDEs

I will summarize some of the recent collaborative work with Le Chen, David Nualart, and Fei Pu in which we characterize when the solution to a large family of parabolic stochastic PDE is ergodic in its spatial variable. We also identify when there are Gaussian fluctuations associated to th

From playlist Columbia SPDE Seminar

Turbulence as Gibbs Statistics of Vortex Sheets - Alexander Migdal

Workshop on Turbulence Topic: Turbulence as Gibbs Statistics of Vortex Sheets Speaker: Alexander Migdal Affiliation: New York University Date: December 11, 2020 For more video please visit http://video.ias.edu

From playlist Mathematics

mandelbrot julia rotation 4

rotation around some two axes at some offset.

From playlist Fractal

Ex 1: Find the Parametric Equations for a Lissajous Curve

This video explains how to determine possible parametric equations for a Lissajous figure. Site: http://mathispower4u.com

From playlist Parametric Equations

Disorder-generated multifractals and random matrices: freezing phenomena and extremes - Yan Fyodorov

Yan Fyodorov Queen Mary University of London October 3, 2013 I will start with discussing the relation between a class of disorder-generated multifractals and logarithmically-correlated random fields and processes. An important example of the latter is provided by the so-called "1/f noise"

From playlist Mathematics

Leonardo da Vinci, Andrei Kolmogorov and Giorgio Parisi. The Energy Decay... by Uriel Frisch

PROGRAM TURBULENCE: PROBLEMS AT THE INTERFACE OF MATHEMATICS AND PHYSICS ORGANIZERS Uriel Frisch (Observatoire de la Côte d'Azur and CNRS, France), Konstantin Khanin (University of Toronto, Canada) and Rahul Pandit (IISc, India) DATE & TIME 16 January 2023 to 27 January 2023 VENUE Ramanuj

From playlist Turbulence: Problems at the Interface of Mathematics and Physics 2023

Optimal shape and location of sensors or actuators in PDE models – Emmanuel Trélat – ICM2018

Control Theory and Optimization Invited Lecture 16.1 Optimal shape and location of sensors or actuators in PDE models Emmanuel Trélat Abstract: We report on a series of works done in collaboration with Y. Privat and E. Zuazua, concerning the problem of optimizing the shape and location o

From playlist Control Theory and Optimization

From order to chaos - Pisa, April, 12 - 2018

Centro di Ricerca Matematica Ennio De Giorgi http://crm.sns.it/event/419/ FROM ORDER TO CHAOS - Pisa 2018 Funded by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement N°647133) and partially supported by GNAMPA-I

From playlist Centro di Ricerca Matematica Ennio De Giorgi

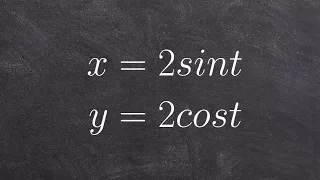
Learn how to eliminate the parameter with trig functions

From playlist Parametric Equations

Parabolic fractal distribution

Related pages