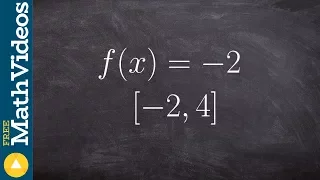
What is the max and min of a horizontal line on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions
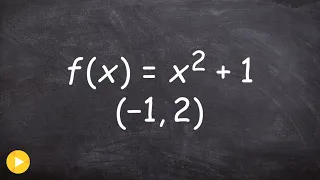
How to determine the absolute max min of a function on an open interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions
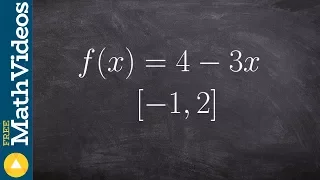
Find the max and min of a linear function on the closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions
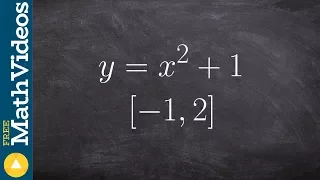
Find the max and min from a quadratic on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

How to determine the global max and min from a piecewise function
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions
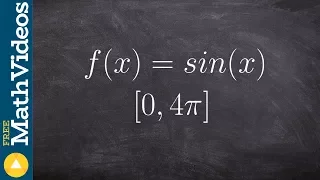
How to determine the max and min of a sine on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Apply the EVT to the square function
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions
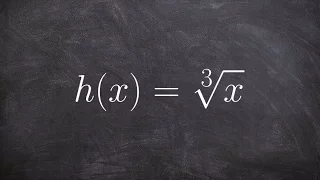
How to apply the evt to a cube root function along a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Bertrand Iooss: Numerical studies of space filling designs: optimization algorithm [...]
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Probability and Statistics

Shannon 100 - 27/10/2016 - Anne AUGER
How information theory sheds new light on black-box optimization Anne Auger (INRIA) Black-box optimization problems occur frequently in many domains ranging from engineering to biology or medicine. In black-box optimization, no information on the function to be optimized besides current
From playlist Shannon 100

Lecture 7 | Convex Optimization I
Professor Stephen Boyd, of the Stanford University Electrical Engineering department, expands upon his previous lectures on convex optimization problems for the course, Convex Optimization I (EE 364A). Convex Optimization I concentrates on recognizing and solving convex optimization pro
From playlist Lecture Collection | Convex Optimization

Stanford ENGR108: Introduction to Applied Linear Algebra | 2020 | Lecture 41-VMLS multi objective LS
Professor Stephen Boyd Samsung Professor in the School of Engineering Director of the Information Systems Laboratory To follow along with the course schedule and syllabus, visit: https://web.stanford.edu/class/engr108/ To view all online courses and programs offered by Stanford, visit:
From playlist Stanford ENGR108: Introduction to Applied Linear Algebra —Vectors, Matrices, and Least Squares

SVD: Optimal Truncation [Matlab]
This video describes how to optimally truncate the singular value decomposition (SVD) for noisy data (Matlab code). See paper by Gavish and Donoho "The Optimal Hard Threshold for Singular Values is 4/\sqrt{3}" https://arxiv.org/abs/1305.5870 https://ieeexplore.ieee.org/document/684629
From playlist Data-Driven Science and Engineering

Sepideh Mirrahimi : Integro-differential models of evolutionary adaptation in changing...- lecture 2
What would be the impact of an environment change on the persistence and the genetic/phenotypic distribution of a population? We present some integro-differential models describing the evolutionary adaptation of asexual phenotypically structured populations subject to mutation and selectio
From playlist CEMRACS 2022

Encouraging Green Architecture in Malaysia
MIT 11.384-11.386 Malaysia Sustainable Cities Program, Spring 2016 View the complete course: http://ocw.mit.edu/11-384S16 Instructor: Shraddha Pandey Shraddha Pandey evaluates the efficacy of Green Building indices and rating systems in creating strong incentives for developers to design
From playlist MIT 11.384-11.386 Malaysia Sustainable Cities Program, Spring 2016

Arthur Krener: "Al'brekht’s Method in Infinite Dimensions"
High Dimensional Hamilton-Jacobi PDEs 2020 Workshop I: High Dimensional Hamilton-Jacobi Methods in Control and Differential Games "Al'brekht’s Method in Infinite Dimensions" Arthur Krener, Naval Postgraduate School Abstract: Al'brekht's method is a way optimally stabilize a finite dimens
From playlist High Dimensional Hamilton-Jacobi PDEs 2020

SVD: Optimal Truncation [Python]
This video describes how to optimally truncate the singular value decomposition (SVD) for noisy data (Python code). See paper by Gavish and Donoho "The Optimal Hard Threshold for Singular Values is 4/\sqrt{3}" https://arxiv.org/abs/1305.5870 https://ieeexplore.ieee.org/document/684629
From playlist Data-Driven Science and Engineering

Determine the extrema using EVT of a rational function
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions
