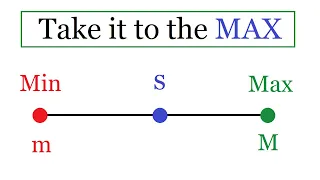
Maximum and Minimum of a set In this video, I define the maximum and minimum of a set, and show that they don't always exist. Enjoy! Check out my Real Numbers Playlist: https://www.youtube.com/playlist?list=PLJb1qAQIrmmCZggpJZvUXnUzaw7fHCtoh
From playlist Real Numbers

Limit of sqrt(9x^6 - x)/(x^3 + 1) as x approaches infinity
Limit of sqrt(9x^6 - x)/(x^3 + 1) as x approaches infinity. We divide the numerator and denominator by the sqruare root of x^6 to do this. Note sqrt(x^6) = x^3 in this problem because x is approaching infinity. If you enjoyed this video please consider liking, sharing, and subscribing. U
From playlist Limits at Infinity

Limit of (4u^4 + 5)/((u^2 - 2)(2u^2 - 1)) as u approaches infinity
Limit of (4u^4 + 5)/((u^2 - 2)(2u^2 - 1)) as u approaches infinity. This is a calculus problem where we find a limit as u approaches infinity. In this case we have a rational function and the numerator and denominator have the same growth rate, so the limit is the ratio of the leading coef
From playlist Limits at Infinity

Easiest Way To Solve an Absolute Value Equation and Determine when Only One Solution
Learn how to solve absolute value equations with extraneous solutions. Absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value problem, we first isolate the absolute value
From playlist Solve Absolute Value Equations

Using parent graphs to understand the left and right hand limits
👉 Learn how to evaluate the limit of an absolute value function. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The absolute value function is a function which only takes the positive val
From playlist Evaluate Limits of Absolute Value

Optimization In this video, I present a very interesting optimization problem, namely I calculate the dimensions of an optimal silo that minimize the cost of building the silo. The catch is that the top dome is more expensive than the lateral part. Enjoy this hour-packed calculus adventur
From playlist Calculus

This video provides an introduction to apportionment. Site: http://mathispower4u.com
From playlist Apportionment

Apportionment: The Alabama Paradox
This video explains and provides an example of the Alabama paradox. Site: http://mathispower4u.com
From playlist Apportionment

Apportionment: Hamilton's Method
This video explains and provides an example of the Hamilton's method of apportionment.. Site: http://mathispower4u.com
From playlist Apportionment
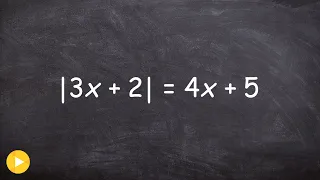
Solving Absolute value equations with a variable on both sides
Learn how to solve absolute value equations with extraneous solutions. Absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value problem, we first isolate the absolute value
From playlist Solve Absolute Value Equations

Apportionment: Huntington-Hill Method
This video explains and provides an example of the Huntington-Hill method of apportionment. Site: http://mathispower4u.com
From playlist Apportionment
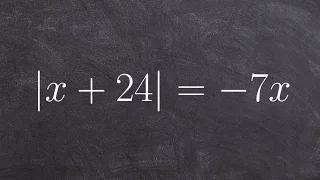
How To Solve an Absolute Value Equation when There is Only One Solution
Learn how to solve absolute value equations with extraneous solutions. Absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value problem, we first isolate the absolute value
From playlist Solve Absolute Value Equations

Apportionment: Webster's Method
This video explains Webster's method of apportionment. Site: http://mathispower4u.com
From playlist Apportionment

Apportionment: Jefferson's Method
This video explains and provides an example of Jefferson's method of apportionment.. Site: http://mathispower4u.com
From playlist Apportionment

Math for Liberal Studies: Apportionment -- Introduction
In this video, we learn the basic concepts we use to solve apportionment problems. Once you have watched this video, you're ready to learn about how to actually solve an apportionment problem using one of the methods below: Hamilton's Method: Jefferson's Method: Adams' Method: Webster's
From playlist Math for Liberal Studies

Apportionment: The New States Paradox
The video explains the new states paradox and provides an example of the population paradox. Site: http://mathispower4u.com
From playlist Apportionment

Evaluate the limit for a value of a function
👉 Learn how to evaluate the limit of an absolute value function. The limit of a function as the input variable of the function tends to a number/value is the number/value which the function approaches at that time. The absolute value function is a function which only takes the positive val
From playlist Evaluate Limits of Absolute Value

Math for Liberal Studies - Lecture 2.7.1 The Apportionment Problem
This is the first video lecture for Math for Liberal Studies Section 2.7: Apportionment. In this video, I give an overview of the apportionment problem: assigning representatives to states based on their population.
From playlist Math for Liberal Studies Lectures

Solving Absolute Value Equations Using Multi Steps
Learn how to solve absolute value equations with extraneous solutions. Absolute value of a number is the positive value of the number. For instance, the absolute value of 2 is 2 and the absolute value of -2 is also 2. To solve an absolute value problem, we first isolate the absolute value
From playlist Solve Absolute Value Equations

Math for Liberal Studies - Lecture 2.7.2 Hamilton's Method and Apportionment Paradoxes
This is the second video lecture for Math for Liberal Studies Section 2.7: Apportionment. In this video, we learn how to use Hamilton's Method to assign a whole number of seats to each state based on their population. We also discuss several "paradoxes" that result from this method.
From playlist Math for Liberal Studies Lectures