
Mike Boyle - Nonnegative matrices : Perron Frobenius theory and related algebra (Part 2)
Nonnegative matrices : Perron Frobenius theory and related algebra (Part 2) Licence: CC BY NC-ND 4.0Lecture I. I’ll give a complete elementary presentation of the essential features of the Perron Frobenius theory of nonnegative matrices for the central case of primitive matrices (the "Perr
From playlist École d’été 2013 - Théorie des nombres et dynamique

Mike Boyle - Nonnegative matrices : Perron Frobenius theory and related algebra (Part 3)
Nonnegative matrices : Perron Frobenius theory and related algebra (Part 3) Licence: CC BY NC-ND 4.0Lecture I. I’ll give a complete elementary presentation of the essential features of the Perron Frobenius theory of nonnegative matrices for the central case of primitive matrices (the "Perr
From playlist École d’été 2013 - Théorie des nombres et dynamique

Mike Boyle - Nonnegative matrices : Perron Frobenius theory and related algebra (Part 1)
Lecture I. I’ll give a complete elementary presentation of the essential features of the Perron Frobenius theory of nonnegative matrices for the central case of primitive matrices (the "Perron" part). (The "Frobenius" part, for irreducible matrices, and finally the case for general nonnega
From playlist École d’été 2013 - Théorie des nombres et dynamique

Mike Boyle - Nonnegative matrices : Perron Frobenius theory and related algebra (Part 4)
Lecture I. I’ll give a complete elementary presentation of the essential features of the Perron Frobenius theory of nonnegative matrices for the central case of primitive matrices (the "Perron" part). (The "Frobenius" part, for irreducible matrices, and finally the case for general nonnega
From playlist École d’été 2013 - Théorie des nombres et dynamique

Determine For Which Matrices and a Given Vector is an Eigenvector
This video explains how to determine if a given vector is a eigenvector for a matrix.
From playlist Eigenvalues and Eigenvectors

Ex: Determine if a 3x3 Matrix is Invertible (nonsingular) Using a Determinant
This video explains how to use a determinant to determine if a 3x3 matrix is invertible. http://mathispower4u.com
From playlist The Determinant of a Matrix

Differential Equations | Undetermined Coefficients for a System of DEs
We use the method of undetermined coefficients to solve a nonhomogeneous system of first order linear differential equations. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Systems of Differential Equations

Lec 19 | MIT 6.046J / 18.410J Introduction to Algorithms (SMA 5503), Fall 2005
Lecture 19: Shortest Paths III: All-pairs Shortest Paths, Matrix Multiplication, Floyd-Warshall, Johnson View the complete course at: http://ocw.mit.edu/6-046JF05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.e
From playlist MIT 6.046J / 18.410J Introduction to Algorithms (SMA 5503),
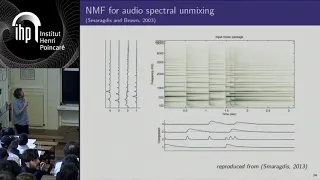
Nonnegative matrix factorisation with the beta-divergence (...) - Févotte - Workshop 3 -CEB T1 2019
Cédric Févotte (CNRS, Toulouse) / 04.04.2019 Nonnegative matrix factorisation with the beta-divergence for robust hyperspectral unmixing Data is often available in matrix form, in which columns are samples, and processing of such data often entails finding an approximate factorisation o
From playlist 2019 - T1 - The Mathematics of Imaging

Differential Equations | Variation of Parameters for a System of DEs
We solve a nonhomogeneous system of linear differential equations using the method of variation of parameters. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Systems of Differential Equations

Jamie Haddock - Hierarchical and neural nonnegative tensor factorizations - IPAM at UCLA
Recorded 02 December 2022. Jamie Haddock of Harvey Mudd College presents "Hierarchical and neural nonnegative tensor factorizations" at IPAM's Multi-Modal Imaging with Deep Learning and Modeling Workshop. Abstract: Nonnegative matrix factorization (NMF) has found many applications includin
From playlist 2022 Multi-Modal Imaging with Deep Learning and Modeling

Simone Cecchini - Distance estimates in the spin setting and the positive mass theorem
The positive mass theorem states that a complete asymptotically Euclidean manifold of nonnegative scalar curvature has nonnegative ADM mass. It relates quantities that are defined using geometric information localized in the Euclidean ends (the ADM mass) with global geometric information o
From playlist Not Only Scalar Curvature Seminar

This video defines a diagonal matrix and then explains how to determine the inverse of a diagonal matrix (if possible) and how to raise a diagonal matrix to a power. Site: mathispower4u.com Blog: mathispower4u.wordpress.com
From playlist Introduction to Matrices and Matrix Operations

What is the domain of square root? - Week 1 - Lecture 5 - Mooculus
Subscribe at http://www.youtube.com/kisonecat
From playlist Ohio State: Jim Fowler's Calculus One Lectures | CosmoLearning Mathematics

Seminar on Applied Geometry and Algebra (SIAM SAGA): Timo de Wolff
Date: Tuesday, March 9 at 11:00am EST (5:00pm CET) Speaker: Timo de Wolff, Technische Universität Braunschweig Title: Certificates of Nonnegativity and Their Applications in Theoretical Computer Science Abstract: Certifying nonnegativity of real, multivariate polynomials is a key proble
From playlist Seminar on Applied Geometry and Algebra (SIAM SAGA)

Example of non-diagonalizable matrix. Exact conditions for a matrix to be (or not to be) diagonalizable. Algebraic and geometric multiplicity of an eigenvalue Check out my Eigenvalues playlist: https://www.youtube.com/watch?v=H-NxPABQlxI&list=PLJb1qAQIrmmC72x-amTHgG-H_5S19jOSf Subscribe
From playlist Eigenvalues