
Learning to simplify a rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions

Simplify a rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions
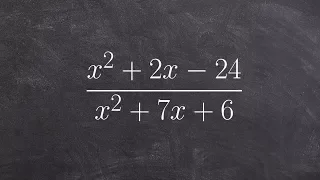
Simplify a rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions

Simplifying a rational expression with a trinomial
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions

Simplify a rational expression by factoring
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions
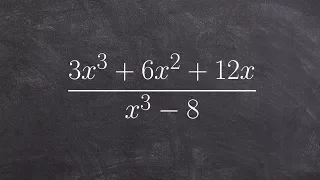
Simplify a rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions

Schemes 14: Irreducible, reduced, integral, connected
This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. We discuss the 4 properties of schemes: reduced, irreducible, integral, and connected.
From playlist Algebraic geometry II: Schemes

This lecture is part of an online graduate course on Lie groups. We state Engel's theorem about nilpotent Lie algebras and sketch a proof of it. We give an example of a nilpotent Lie group that is not a matrix group. For the other lectures in the course see https://www.youtube.com/play
From playlist Lie groups

Commutative algebra 30 Symbolic powers
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we give some examples related to primary ideals. In particular we give an example of a primary ideal that is
From playlist Commutative algebra

Simplify a rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions (Binomials) #Rational

Commutative algebra 31 (Nullstellensatz)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We describe the weak and strong Nullstellensatz, and give short proofs of them over the complex numbers using Rabinowitsch's
From playlist Commutative algebra

Commutative algebra 26 (Examples of Artinian rings)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we give some examples or Artin rings and write them as products of local rings. The examples include some Arti
From playlist Commutative algebra

Commutative algebra 18 (Functions on Spec R)
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we explain how to consider elements of a ring R as functions on the space Spec R, taking values at each point
From playlist Commutative algebra

An general explanation of the underactive thyroid.
From playlist For Patients

This lecture is part of an online graduate course on Lie groups. This lecture is about Lie's theorem, which implies that a complex solvable Lie algebra is isomorphic to a subalgebra of the upper triangular matrices. . For the other lectures in the course see https://www.youtube.com/playl
From playlist Lie groups

Commutative algebra 61: Examples of regular local rings
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We give some examples of regular local rings. We first give an example of a regular local ring that is not geometrically regul
From playlist Commutative algebra

Simplify a rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions (Binomials) #Rational

Commutative algebra 29 The Lasker Noether theorem
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We state and prove three versions of the Lasker-Noether theorem, the first expressing an ideal as an intersection of primary
From playlist Commutative algebra
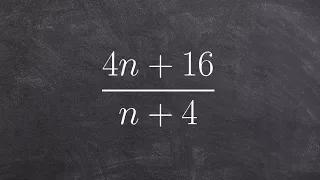
Simplifying rational expression
Learn how to simplify rational expressions. A rational expression is an expression in the form of a fraction where the numerator and/or the denominator are/is an algebraic expression. To simplify a rational expression, we factor completely the numerator and the denominator of the rational
From playlist Simplify Rational Expressions (Binomials) #Rational
