
The Fundamental Theorem of Calculus | Algebraic Calculus One | Wild Egg
In this video we lay out the Fundamental Theorem of Calculus --from the point of view of the Algebraic Calculus. This key result, presented here for the very first time (!), shows how to generalize the Fundamental Formula of the Calculus which we presented a few videos ago, incorporating t
From playlist Algebraic Calculus One

Ptolemy's theorem and generalizations | Rational Geometry Math Foundations 131 | NJ Wildberger
The other famous classical theorem about cyclic quadrilaterals is due to the great Greek astronomer and mathematician, Claudius Ptolemy. Adopting a rational point of view, we need to rethink this theorem to state it in a purely algebraic way, without resort to `distances' and the correspon
From playlist Math Foundations

Proof of Lemma and Lagrange's Theorem
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proof of Lemma and Lagrange's Theorem. This video starts by proving that any two right cosets have the same cardinality. Then we prove Lagrange's Theorem which says that if H is a subgroup of a finite group G then the order of H div
From playlist Abstract Algebra

Calculus - The Fundamental Theorem, Part 1
The Fundamental Theorem of Calculus. First video in a short series on the topic. The theorem is stated and two simple examples are worked.
From playlist Calculus - The Fundamental Theorem of Calculus

Theory of numbers: Congruences: Euler's theorem
This lecture is part of an online undergraduate course on the theory of numbers. We prove Euler's theorem, a generalization of Fermat's theorem to non-prime moduli, by using Lagrange's theorem and group theory. As an application of Fermat's theorem we show there are infinitely many prim
From playlist Theory of numbers

Unbounded Fast Escaping Wandering Domains - Adi Glücksam
Special Year Research Seminar Topic: Unbounded Fast Escaping Wandering Domains Speaker: Adi Glücksam Affiliation: Northwestern University Date: March 21, 2023 Complex dynamics explores the evolution of points under iteration of functions of complex variables. In this talk I will introduc
From playlist Mathematics

R. Dujardin - Some problems of arithmetic origin in complex dynamics and geometry (part1)
Some themes inspired from number theory have been playing an important role in holomorphic and algebraic dynamics (iteration of rational mappings) in the past ten years. In these lectures I would like to present a few recent results in this direction. This should include: the dynamica
From playlist Ecole d'été 2017 - Géométrie d'Arakelov et applications diophantiennes
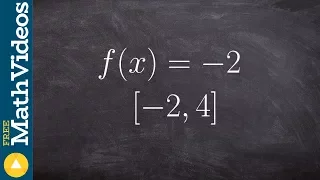
What is the max and min of a horizontal line on a closed interval
👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points
From playlist Extreme Value Theorem of Functions

Calculus 5.3 The Fundamental Theorem of Calculus
My notes are available at http://asherbroberts.com/ (so you can write along with me). Calculus: Early Transcendentals 8th Edition by James Stewart
From playlist Calculus

R. Dujardin - Some problems of arithmetic origin in complex dynamics and geometry (part3)
Some themes inspired from number theory have been playing an important role in holomorphic and algebraic dynamics (iteration of rational mappings) in the past ten years. In these lectures I would like to present a few recent results in this direction. This should include: the dynamica
From playlist Ecole d'été 2017 - Géométrie d'Arakelov et applications diophantiennes

R. Dujardin - Some problems of arithmetic origin in complex dynamics and geometry (part2)
Some themes inspired from number theory have been playing an important role in holomorphic and algebraic dynamics (iteration of rational mappings) in the past ten years. In these lectures I would like to present a few recent results in this direction. This should include: the dynamica
From playlist Ecole d'été 2017 - Géométrie d'Arakelov et applications diophantiennes

Sums of Squares Over k-Subset Hypercubes - Annie Raymond
Computer Science/Discrete Mathematics Seminar I Topic: Sums of Squares Over k-Subset Hypercubes Speaker: Annie Raymond Affiliation: University of Massachusetts, Amherst Date: April 16, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Proof of the Fundamental Theorem of Calculus (Part 1)
This video proves the Fundamental Theorem of Calculus (Part 1). http://mathispower4u.com
From playlist The Second Fundamental Theorem of Calculus

Lecture 19: Identification and Falsification
MIT 14.04 Intermediate Microeconomic Theory, Fall 2020 Instructor: Prof. Robert Townsend View the complete course: https://ocw.mit.edu/courses/14-04-intermediate-microeconomic-theory-fall-2020/ YouTube Playlist: https://www.youtube.com/watch?v=XSTSfCs74bg&list=PLUl4u3cNGP63wnrKge9vllow3Y2
From playlist MIT 14.04 Intermediate Microeconomic Theory, Fall 2020

Session Three: Exciting and Ongoing Developments
Panel: Will Rosenzweig, Christopher Gardner, Eric Montell, Greg Drescher
From playlist Stanford Food Summit

Dror Varolin - Minicourse - Lecture 2
Dror Varolin Variations of Holomorphic Hilbert spaces Traditional complex analysis focuses on a single space, like a domain in Euclidean space, or more generally a complex manifold, and studies holomorphic maps on that space, into some target space. The typical target space for a domain i
From playlist Maryland Analysis and Geometry Atelier

Number Theory | A very special case of Fermat's Last Theorem
We prove a very simple case of Fermat's Last Theorem. Interestingly, this case is fairly easy to prove which highlights the allure of the theorem as a whole -- especially given the fact that much of modern number theory was developed as part of the program that ended in the full proof. ht
From playlist Number Theory

Theory of numbers: Fermat's theorem
This lecture is part of an online undergraduate course on the theory of numbers. We prove Fermat's theorem a^p = a mod p. We then define the order of a number mod p and use Fermat's theorem to show the order of a divides p-1. We apply this to testing some Fermat and Mersenne numbers to se
From playlist Theory of numbers

Alexandru Dimca, Research talk - 10 February 2015
Alexandru Dimca (Université de Nice Sophia Antipolis, France) - Research talk http://www.crm.sns.it/course/4384/ We report on recent results relating the syzygies involving the partial derivatives of a homogeneous polynomial f to the geometry of the projective hypersurface f=0 and the ass
From playlist Algebraic topology, geometric and combinatorial group theory - 2015
