
The Lie-algebra of Quaternion algebras and their Lie-subalgebras
In this video we discuss the Lie-algebras of general quaternion algebras over general fields, especially as the Lie-algebra is naturally given for 2x2 representations. The video follows a longer video I previously did on quaternions, but this time I focus on the Lie-algebra operation. I st
From playlist Algebra

In this video I write down the axioms of Lie algebras and then discuss the defining anti-symmetric bilinear map (the Lie bracket) which is zero on the diagonal and fulfills the Jacobi identity. I'm following the compact book "Introduction to Lie Algebras" by Erdmann and Wildon. https://gi
From playlist Algebra

The Weyl algebra and the Heisenberg Lie algebra
In this video we give a simple teaser into the world of operator algebras. In particular, we talk about the Weyl algebra and compute some expressions that fulfill the property which defines the Heisenberg Lie algebra http://math.uchicago.edu/~may/REU2012/REUPapers/Lingle.pdf https://en.w
From playlist Algebra

This lecture is part of an online graduate course on Lie groups. We define the Lie algebra of a Lie group in two ways, and show that it satisfied the Jacobi identity. The we calculate the Lie algebras of a few Lie groups. For the other lectures in the course see https://www.youtube.co
From playlist Lie groups

In this clip I casually give a roundup of some of my current interests and also recommend you some literature. Get into Lie algebras, Lie groups and algebraic groups. Do it now! https://en.wikipedia.org/wiki/Lie_algebra http://www.jmilne.org/math/index.html
From playlist Algebra

Lie groups: Lie groups and Lie algebras
This lecture is part of an online graduate course on Lie groups. We discuss the relation between Lie groups and Lie algebras, and give several examples showing how they behave differently. Lie algebras turn out to correspond more closely to the simply connected Lie groups. We then explain
From playlist Lie groups

RNT1.4. Ideals and Quotient Rings
Ring Theory: We define ideals in rings as an analogue of normal subgroups in group theory. We give a correspondence between (two-sided) ideals and kernels of homomorphisms using quotient rings. We also state the First Isomorphism Theorem for Rings and give examples.
From playlist Abstract Algebra

Lie groups: Poincare-Birkhoff-Witt theorem
This lecture is part of an online graduate course on Lie groups. We state the Poincare-Birkhoff Witt theorem, which shows that the universal enveloping algebra (UEA) of a Lie algebra is the same size as a polynomial algebra. We prove it for Lie algebras of Lie groups and sketch a proof of
From playlist Lie groups
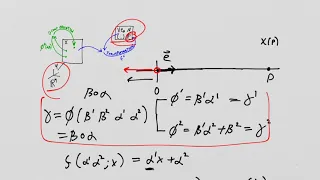
Lie Groups and Lie Algebras: Lesson 16 - representations, connectedness, definition of Lie Group
Lie Groups and Lie Algebras: Lesson 16 - representations, connectedness, definition of Lie Group We cover a few concepts in this lecture: 1) we introduce the idea of a matrix representation using our super-simple example of a continuous group, 2) we discuss "connectedness" and explain tha
From playlist Lie Groups and Lie Algebras

Math talk: Sporadic groups and number theory
This talk was the introduction to the Berkeley graduate number theory discussion seminar on 2020-10-28, and the aim was to explain why number theorists might be interested in sporadic simple groups. We give a brief summary of monstrous moonshine relating sporadic groups to modular functi
From playlist Math talks

Simple Groups - Abstract Algebra
Simple groups are the building blocks of finite groups. After decades of hard work, mathematicians have finally classified all finite simple groups. Today we talk about why simple groups are so important, and then cover the four main classes of simple groups: cyclic groups of prime order
From playlist Abstract Algebra

A guide to moonshine - John Duncan
Celebration In Honor of the Frank C. and Florence S. Ogg Professorship Topic: A guide to moonshine Speaker: John Duncan Affiliation: Associate Professor, Emory University and Research Fellow, Academia Sinica Date: October 13, 2022 J. Duncan will explain how the works of Andrew Ogg—especi
From playlist Mathematics

Some reasons why vertex algebras are interesting.
We give some reasons why anyone would want to study vertex algebras. We include their connection to group theory, number theory, and mathematical physics. More VOAs on youtube: https://www.youtube.com/c/seandownes/playlists Please Subscribe: https://www.youtube.com/michaelpennmath?sub_co
From playlist Vertex Operator Algebras

Simple grps 1 by N. S. Narasimha Sastry
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

Simple groups, Lie groups, and the search for symmetry II | Math History | NJ Wildberger
This is the second video in this lecture on simple groups, Lie groups and manifestations of symmetry. During the 19th century, the role of groups shifted from its origin in number theory and the theory of equations to its role in describing symmetry in geometry. In this video we talk abou
From playlist MathHistory: A course in the History of Mathematics

Claudia Pinzari: "Weak quasi-Hopf algebras associated to Verlinde fusion categories"
Actions of Tensor Categories on C*-algebras 2021 "Weak quasi-Hopf algebras associated to Verlinde fusion categories" Claudia Pinzari - Sapienza Università di Roma Abstract: Unitary modular fusion categories arise in various frameworks. After a general overview on unitarity, we discuss th
From playlist Actions of Tensor Categories on C*-algebras 2021

Simple groups, Lie groups, and the search for symmetry I | Math History | NJ Wildberger
During the 19th century, group theory shifted from its origins in number theory and the theory of equations to describing symmetry in geometry. In this video we talk about the history of the search for simple groups, the role of symmetry in tesselations, both Euclidean, spherical and hyper
From playlist MathHistory: A course in the History of Mathematics

Moonshine - 2 by Suresh Govindarajan
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods

Lie Groups and Lie Algebras: Lesson 18- Group Generators
Lie Groups and Lie Algebras: Lesson 18- Generators This is an important lecture! We work through the calculus of *group generators* and walk step-by-step through the exploitation of analyticity. That is, we use the Taylor expansion of the continuous functions associated with a Lie group o
From playlist Lie Groups and Lie Algebras

Imprimitive irreducible representations of finite quasisimple groups by Gerhard Hiss
DATE & TIME 05 November 2016 to 14 November 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Computational techniques are of great help in dealing with substantial, otherwise intractable examples, possibly leading to further structural insights and the detection of patterns in many abstra
From playlist Group Theory and Computational Methods