
Modular Forms | Modular Forms; Section 1 2
We define modular forms, and borrow an idea from representation theory to construct some examples. My Twitter: https://twitter.com/KristapsBalodi3 Fourier Theory (0:00) Definition of Modular Forms (8:02) In Search of Modularity (11:38) The Eisenstein Series (18:25)
From playlist Modular Forms

This lecture is part of an online graduate course on modular forms. We introduce modular forms, and give several examples of how they were used to solve problems in apparently unrelated areas of mathematics. I will not be following any particular book, but if anyone wants a suggestion
From playlist Modular forms

Modular forms: Eisenstein series
This lecture is part of an online graduate course on modular forms. We give two ways of looking at modular forms: as functions of lattices in C, or as invariant forms. We use this to give two different ways of constructing Eisenstein series. For the other lectures in the course see http
From playlist Modular forms

Modular Functions | Modular Forms; Section 1.1
In this video we introduce the notion of modular functions. My Twitter: https://twitter.com/KristapsBalodi3 Intro (0:00) Weakly Modular Functions (2:10) Factor of Automorphy (8:58) Checking the Generators (15:04) The Nome Map (16:35) Modular Functions (22:10)
From playlist Modular Forms

This lecture is part of an online graduate course on modular forms. We first show that the number of zeros of a (level 1 holomorphic) modular form in a fundamental domain is weight/12, and use this to show that the graded ring of modular forms is the ring of polynomials in E4 and E6. Fo
From playlist Modular forms

Modular forms: Modular functions
This lecture is part of an online graduate course on modular forms. We classify all meromorphic modular functions, showing that they are all rational functions of the elliptic modular function j. As an application of j we use it to prove Picard's theorem that a non-constant meromorphic
From playlist Modular forms

Weakly Modular Functions | The Geometry of SL2,Z, Section 1.4
We provide an alternative motivation for the definition of weakly modular functions. My Twitter: https://twitter.com/KristapsBalodi3 Weakly Modular Functions (0:00) Boring Functions on Compact Riemann Surfaces (2:06) Transforming the Transformation Property (9:15)
From playlist The Geometry of SL(2,Z)

Modular forms: Fundamental domain
This lecture is part of an online graduate course on modular forms. We describe the fundamental domain of SL2(Z) acting on the upper half plane. For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj51HisRtNyzHX-Xyg6I3Wl2F
From playlist Modular forms

Modular forms: Theta functions in higher dimensions
This lecture is part of an online graduate course on modular forms. We study theta functions of even unimodular lattices, such as the root lattice of the E8 exceptional Lie algebra. As examples we show that one cannot "her the shape of a drum", and calculate the number of minimal vectors
From playlist Modular forms

“Mock and Quantum Modular Forms” by Amanda Folsom (Part 2 of 2)
“Mock and Quantum Modular Forms” by Amanda Folsom (Amherst College). This is a video from CTNT, the Connecticut Summer School in Number Theory that took place at UConn during August 8th - 14th, 2016, organized by Keith Conrad, Amanda Folsom, Alvaro Lozano-Robledo, and Liang Xiao. For more
From playlist CTNT 2016 - “Mock and Quantum Modular Forms” by Amanda Folsom

“Mock and Quantum Modular Forms” by Amanda Folsom (Part 1 of 2)
“Mock and Quantum Modular Forms” by Amanda Folsom (Amherst College). This is a video from CTNT, the Connecticut Summer School in Number Theory that took place at UConn during August 8th - 14th, 2016, organized by Keith Conrad, Amanda Folsom, Alvaro Lozano-Robledo, and Liang Xiao. For more
From playlist CTNT 2016 - “Mock and Quantum Modular Forms” by Amanda Folsom

Niebur Integrals and Mock Automorphic Forms - Wladimir de Azevedo Pribitkin
Wladimir de Azevedo Pribitkin College of Staten Island, CUNY March 17, 2011 Among the bounty of brilliancies bequeathed to humanity by Srinivasa Ramanujan, the circle method and the notion of mock theta functions strike wonder and spark intrigue in number theorists fresh and seasoned alike
From playlist Mathematics

Karl Mahlburg: Automorphic forms and classical partition identities
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Number Theory

Math talk: Sporadic groups and number theory
This talk was the introduction to the Berkeley graduate number theory discussion seminar on 2020-10-28, and the aim was to explain why number theorists might be interested in sporadic simple groups. We give a brief summary of monstrous moonshine relating sporadic groups to modular functi
From playlist Math talks
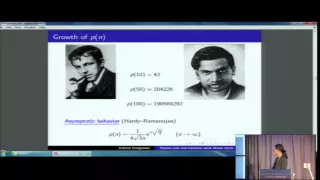
Dyson's Rank, Harmonic Weak Maass Form, and Recent Developments - Kathrin Bringmann
Kathrin Bringmann University of Cologne September 27, 2013 More videos on http://video.ias.edu
From playlist Dreams of Earth and Sky

Sander Zwegers: Fourier coefficients of meromorphic Jacobi forms
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist SPECIAL 7th European congress of Mathematics Berlin 2016.
Topological and arithmetic intersection numbers attached to real quadratic cycles -Henri Darmon
Workshop on Motives, Galois Representations and Cohomology Around the Langlands Program Topic: Topological and arithmetic intersection numbers attached to real quadratic cycles Speaker: Henri Darmon Affiliation: McGill University Date: November 8, 2017 For more videos, please visit http
From playlist Mathematics

Minoru Wakimoto, Mock modular forms and representation theory of affine Lie superalgebras
Minoru WAKIMOTO (Université de Kyushu) "Mock modular forms and representation theory of affine Lie superalgebras - the case of sl(2|1)^"
From playlist Après-midi en l'honneur de Victor KAC

Introduction to Modular Forms - Part 1 of 8
“Introduction to Modular Forms,” by Keith Conrad. Topics include Eisenstein series and q-expansions, applications to sums of squares and zeta-values, Hecke operators, eigenforms, and the L-function of a modular form. This is a video from CTNT, the Connecticut Summer School in Number Theor
From playlist CTNT 2016 - "Introduction to Modular Forms" by Keith Conrad

A guide to moonshine - John Duncan
Celebration In Honor of the Frank C. and Florence S. Ogg Professorship Topic: A guide to moonshine Speaker: John Duncan Affiliation: Associate Professor, Emory University and Research Fellow, Academia Sinica Date: October 13, 2022 J. Duncan will explain how the works of Andrew Ogg—especi
From playlist Mathematics