
B01 An introduction to numerical methods
Most differential equations cannot be solved by the analytical techniques that we have learned up until now. I these cases, we can approximate a solution by a set of points, by using a variety of numerical methods. The first of these is Euler's method.
From playlist A Second Course in Differential Equations

Solving a system of equations with infinite many solutions
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium

Solve a System of Linear Equations Using Elimination
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium
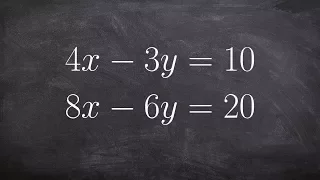
Solve a System of Linear Equations Using Elimination
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium

Solve a System of Linear Equations Using Elimination
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium

Solve a System of Linear Equations Using Elimination
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium
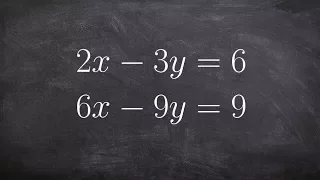
Labeling a System by Solving Using Elimination Method
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium

Mod-01 Lec-01 Introduction and Overview
Advanced Numerical Analysis by Prof. Sachin C. Patwardhan,Department of Chemical Engineering,IIT Bombay.For more details on NPTEL visit http://nptel.ac.in
From playlist IIT Bombay: Advanced Numerical Analysis | CosmoLearning.org

Lec 29 | MIT 18.03 Differential Equations, Spring 2006
Matrix Exponentials; Application to Solving Systems. View the complete course: http://ocw.mit.edu/18-03S06 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 18.03SC Differential Equations, Fall 2011

MIT 10.34 Numerical Methods Applied to Chemical Engineering, Fall 2015 View the complete course: http://ocw.mit.edu/10-34F15 Instructor: James Swan This session dedicated to a review of all different numerical methods students learned from this course. License: Creative Commons BY-NC-SA
From playlist MIT 10.34 Numerical Methods Applied to Chemical Engineering, Fall 2015

Solving a System by Using a Multiplier for Elimination
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium

Giuseppe Mingione - 23 September 2016
Mingione, Giuseppe "Recent progresses in nonlinear potential theory"
From playlist A Mathematical Tribute to Ennio De Giorgi
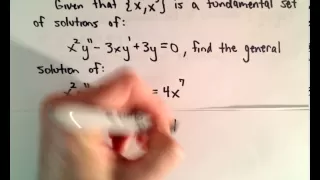
Variation of Parameters to Solve a Differential Equation (Second Order)
Thanks to all of you who support me on Patreon. You da real mvps! $1 per month helps!! :) https://www.patreon.com/patrickjmt !! THE VIDEO ENDS ABRUPTLY, BUT THERE WAS NOTHING IMPORTANT THERE :) Variation of Parameters to Solve a Differential Equation (Second Order). In this video, I gi
From playlist All Videos - Part 1
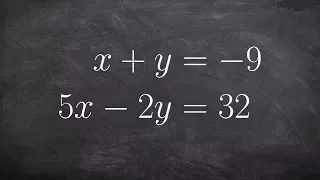
Solve a System of Equations by Using Elimination of Multiplying
👉Learn how to solve a system (of equations) by elimination. A system of equations is a set of equations which are collectively satisfied by one solution of the variables. The elimination method of solving a system of equations involves making the coefficient of one of the variables to be e
From playlist Solve a System of Equations Using Elimination | Medium

Michael Atiyah: Poincaré conjecture, Hodge conjecture, Yang-Mills, Navier-Stokes [2000]
Millennium Meeting These videos document the Institute's landmark Paris millennium event which took place on May 24-25, 2000, at the Collège de France. On this occasion, CMI unveiled the "Millennium Prize Problems," seven mathematical quandaries that have long resisted solution. The announ
From playlist Number Theory

Sascha Husa (4) - Introduction to theory and numerics of partial differential equations
PROGRAM: NUMERICAL RELATIVITY DATES: Monday 10 Jun, 2013 - Friday 05 Jul, 2013 VENUE: ICTS-TIFR, IISc Campus, Bangalore DETAL Numerical relativity deals with solving Einstein's field equations using supercomputers. Numerical relativity is an essential tool for the accurate modeling of a wi
From playlist Numerical Relativity

Marina Poulet, Université Claude Bernard Lyon 1
December 9, Marina Poulet, Université Claude Bernard Lyon 1 Zariski-dense subgroups of Galois groups for Mahler equations
From playlist Fall 2021 Online Kolchin Seminar in Differential Algebra

2023 Number Challenge: Pell's Equation with d=2023
Check out other 2023 Number Challenges from this list. Share with your friends!! https://www.youtube.com/playlist?list=PLXpXgWDr4HM7KKeX7CaQIu4tfPRJ2HiUM Please subscribe to the channel. In this video, we study Pell's equation when d=2023. We use two methods: 1. With continue continu
From playlist Math Problems with Number 2023

Sergiu Klainerman - 3/4 On the Mathematical Theory of Black Holes
https://indico.math.cnrs.fr/event/3463/ The gravitational waves detected by LIGO were produced in the final faze of the inward spiraling of two black holes before they collided to produce a more massive black hole. The experiment is entirely consistent with the so called Final State Conjec
From playlist Sergiu Klainerman - On the Mathematical Theory of Black Holes

Differential Equation - 2nd Order Linear (4 of 17) The Fundamental Theory
Visit http://ilectureonline.com for more math and science lectures! In this video I will introduce and explain the Fundamental Theory for the solution to 2nd order linear homogeneous differential equations. Next video in the series can be seen at: http://youtu.be/oItnzOZsayA
From playlist DIFFERENTIAL EQUATIONS 9 - 2nd ORDER INTRODUCTION