
Mertens Conjecture Disproof and the Riemann Hypothesis | MegaFavNumbers
#MegaFavNumbers The Mertens conjecture is a conjecture is a conjecture about the distribution of the prime numbers. It can be seen as a stronger version of the Riemann hypothesis. It says that the Mertens function is bounded by sqrt(n). The Riemann hypothesis on the other hand only require
From playlist MegaFavNumbers

From playlist Cryptography

More resources available at www.misterwootube.com
From playlist The Nature of Proof

My #MegaFavNumbers is 2^82589933-1 // The largest Mersenne prime…..yet
This video is part of the #MegaFavNumbers series where a tonne of math youtubers like @numberphile @standupmaths and @3blue1brown share their favourite MEGA numbers, i.e. numbers over a million. Check out the full playlist here: https://www.youtube.com/playlist?list=PLar4u0v66vIodqt3KSZPs
From playlist MegaFavNumbers
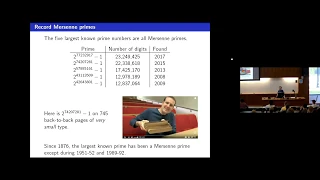
CTNT 2018 - "The Biggest Known Prime Number" by Keith Conrad
This is lecture on "The Biggest Known Prime Number", by Keith Conrad, during CTNT 2018, the Connecticut Summer School in Number Theory. For more information about CTNT and other resources and notes, see https://ctnt-summer.math.uconn.edu/
From playlist CTNT 2018 - Guest Lectures
The Biggest Known Prime Number - Keith Conrad [2018]
Slides for this talk: https://ctnt-summer.math.uconn.edu/wp-content/uploads/sites/1632/2018/05/mersennetalkCTNT.pdf May 29: Keith Conrad (UConn) Title: The Biggest Known Prime Number. Abstract: There are infinitely many primes, but at any moment there is a biggest known prime. Earlier t
From playlist Number Theory

What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics

Frank Merle - 1/4 Comportement asymptotique des solutions de l'équation des ondes critique
Les principales questions abordées dans cette série de cours concernent l'existence locale et globale en temps, explosion en temps fini et la résolution en solitons des solutions de l'équation des ondes non linéaire énergie critique. Les lectures ne demanderont pas de pré-requis.
From playlist Frank Merle - Comportement asymptotique des solutions de

Fundamentals of Mathematics - Lecture 09: What you can't do with Groups; Special primes.
course page: http://www.uvm.edu/~tdupuy/logic/Math52-Fall2017.html handouts - DZB, Emory videography - Eric Melton, UVM
From playlist Fundamentals of Mathematics

Primes, Complexity and Computation: How Big Number theory resolves the Goldbach Conjecture
This lecture, which begins at 2:45, shows how Big Number theory, together with an understanding of prime numbers and their distribution resolves the Goldbach Conjecture, which states that every even number greater than two is the sum of two primes. Notions of complexity and computation,
From playlist MathSeminars

Frank Merle - 3/4 Comportement asymptotique des solutions de l'équation des ondes critique
Les principales questions abordées dans cette série de cours concernent l'existence locale et globale en temps, explosion en temps fini et la résolution en solitons des solutions de l'équation des ondes non linéaire énergie critique. Les lectures ne demanderont pas de pré-requis.
From playlist Frank Merle - Comportement asymptotique des solutions de

Primes without a 7 - Numberphile
James Maynard discusses his proof that infinite primes exist missing each base 10 digit - he uses 7 as his arbitrary example. More links & stuff in full description below ↓↓↓ More videos with James Maynard: http://bit.ly/JamesMaynard The paper on primes with restricted digits: https://ar
From playlist James Maynard on Numberphile

Frank Merle - 4/4 Comportement asymptotique des solutions de l'équation des ondes critique
Les principales questions abordées dans cette série de cours concernent l'existence locale et globale en temps, explosion en temps fini et la résolution en solitons des solutions de l'équation des ondes non linéaire énergie critique. Les lectures ne demanderont pas de pré-requis.
From playlist Frank Merle - Comportement asymptotique des solutions de

Prime numbers, Ulam Spirals and other cool numbery stuff with Dr James Grime. More links & stuff in full description below ↓↓↓ James Clewett on spirals at: http://youtu.be/3K-12i0jclM And more to come soon... * subscribing to numberphile does not really change your physical appearance!
From playlist James Grime on Numberphile
Combinatorial affine sieve - Alireza Salehi Golsefidy
Speaker: Alireza Salehi Golsefidy (UCSD) Title: Combinatorial affine sieve Abstract: In this talk the general setting of affine sieve will be presented. Next I will explain the Bourgain-Gamburd-Sarnak method on proving affine sieve in the presence of certain spectral gap. Finally I will sa
From playlist Mathematics

Euclid's Perfects and Mersenne's Primes (visually)
In this video, we show a visual proof of a theorem first proved by Euclid. The theorem states that if 2 raised to the p minus 1 is prime, then 2 raised to the (p-1) multiplied by that prime must be perfect. We end with some commentary about perfect numbers and primes of this special form (
From playlist Proof Writing

7 is the only Prime followed by a Cube.
Feel like exploring more curious facts about prime numbers? Why not try out Brilliant then? =D https://brilliant.org/FlammableMaths Hagoromo chalk :D https://stemerch.com/collections/school-teaching-supplies Infimum Merch :0 https://papaflammy.creator-spring.com/listing/infimum? Today we
From playlist Number Theory
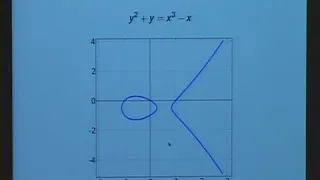
Solutions to Cubic Equations - Benedict Gross (Harvard University)
Beginning with some simple principles that go back to the ancient Greeks for solving some low-degree equations, we will then turn to some basic questions raised by Euler and Fermat, whose answers have led to surprising applications (secure Internet commerce) as well as to the solution of f
From playlist Mathematics Research Center

Why are Mersenne primes and perfect number related? | SoME contest entry
In this video, I explain how Mersenne primes are related to perfect numbers, go over the Euclid half of the Euclid-Euler theorem, and make a bunch of really terrible "jokes". This video is my submission to the 3Blue1Brown Summer of Math Exposition contest. Consider checking out some other
From playlist Summer of Math Exposition Youtube Videos
