
What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics

Watch more videos on http://www.brightstorm.com/math/geometry SUBSCRIBE FOR All OUR VIDEOS! https://www.youtube.com/subscription_center?add_user=brightstorm2 VISIT BRIGHTSTORM.com FOR TONS OF VIDEO TUTORIALS AND OTHER FEATURES! http://www.brightstorm.com/ LET'S CONNECT! Facebook ► https
From playlist Geometry

The Campbell-Baker-Hausdorff and Dynkin formula and its finite nature
In this video explain, implement and numerically validate all the nice formulas popping up from math behind the theorem of Campbell, Baker, Hausdorff and Dynkin, usually a.k.a. Baker-Campbell-Hausdorff formula. Here's the TeX and python code: https://gist.github.com/Nikolaj-K/8e9a345e4c932
From playlist Algebra

In this video I write down the axioms of Lie algebras and then discuss the defining anti-symmetric bilinear map (the Lie bracket) which is zero on the diagonal and fulfills the Jacobi identity. I'm following the compact book "Introduction to Lie Algebras" by Erdmann and Wildon. https://gi
From playlist Algebra

Asymptotic enumeration of graphs with given degree sequence – Nicholas Wormald – ICM2018
Combinatorics Invited Lecture 13.7 Asymptotic enumeration of graphs with given degree sequence Nicholas Wormald Abstract: We survey results on counting graphs with given degree sequence, focusing on asymptotic results, and mentioning some of the applications of these results. The main re
From playlist Combinatorics

The Fundamental Theorem of Calculus | Algebraic Calculus One | Wild Egg
In this video we lay out the Fundamental Theorem of Calculus --from the point of view of the Algebraic Calculus. This key result, presented here for the very first time (!), shows how to generalize the Fundamental Formula of the Calculus which we presented a few videos ago, incorporating t
From playlist Algebraic Calculus One
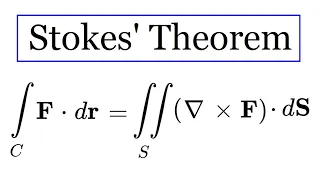
In this video, I present another example of Stokes theorem, this time using it to calculate the line integral of a vector field. It is a very useful theorem that arises a lot in physics, for example in Maxwell's equations. Other Stokes Example: https://youtu.be/-fYbBSiqvUw Yet another Sto
From playlist Vector Calculus
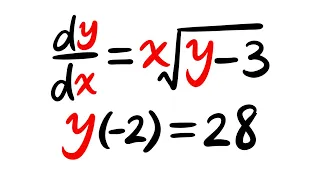
Existence & Uniqueness Theorem, Ex1.5
Existence & Uniqueness Theorem for differential equations. Subscribe for more math for fun videos 👉 https://bit.ly/3o2fMNo For more calculus & differential equation tutorials, check out @justcalculus 👉 https://www.youtube.com/justcalculus To learn how to solve different types of d
From playlist Differential Equations: Existence & Uniqueness Theorem (Nagle Sect1.2)

Lie Fu: Multiplicative McKay correspondence for surfaces
30 September 2021 Abstract: Given a nite subgroup of SL(2,C), the classical 2-dimensional McKay correspondence provides a connection between the representation theory of the group and the exceptional divisor of the minimal resolution of the quotient singularity that the group naturally gi
From playlist Representation theory's hidden motives (SMRI & Uni of Münster)

CSDM: Finding Needles in Exponential Haystacks - Joel Spencer
Joel Spencer Courant Institute, NYU February 21, 2012 For more videos, visit http://video.ias.edu
From playlist Mathematics

Chris McKay: Results of the Phoenix Mission to Mars and Analog Sites on Earth
Google Tech Talks October 6, 2008 ABSTRACT Phoenix landed at 68N in the ice-rich ground on Mars and investigated the chemistry and geology of a polar site on Mars for the first time. The site is particularly interesting for astrobiology because 5 Myr ago the tilt of Mars' axis was 4
From playlist NASA Speakers at Google

Fun with Graphs: Rock Paper Scissors Lizard Spock - (part 2)
Rock-Paper-Scissors-Lizard-Spock and Other Uses for the Complete Graph (part 2) A talk by Dr. Sarada Herke If you have ever played Rock-Paper-Scissors, then you have actually played with a complete graph (yes, a very small one). In this 6-part talk we will look at generalisations of this
From playlist Fun with Graphs: Rock Paper Scissors Lizard Spock
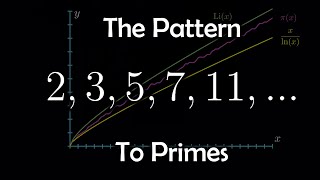
In this video, we explore the "pattern" to prime numbers. I go over the Euler product formula, the prime number theorem and the connection between the Riemann zeta function and primes. Here's a video on a similar topic by Numberphile if you're interested: https://youtu.be/uvMGZb0Suyc The
From playlist Other Math Videos

Representations of finite groups and applications – Pham Huu Tiep – ICM2018
Algebra Invited Lecture 2.4 Representations of finite groups and applications Pham Huu Tiep Abstract: We discuss some basic problems in representation theory of finite groups, and current approaches and recent progress on some of these problems. We will also outline some applications of
From playlist Algebra

Who Really Wrote The Count of Monte Cristo? - So You Haven't Read - #Shorts
The Count of Monte Cristo was one of Alexandre Dumas' towering literary achievements. However, did you know Ghost Writer Auguste Maquet had a hand in writing the popular novel? ---- The Count of Monte Cristo Episode ---- https://youtu.be/ZZZHOyZiLNU ---- Thanks for participating in this
From playlist So You Haven't Read (ALL EPISODES)

Peter SCHOLZE (oct 2011) - 6/6 Perfectoid Spaces and the Weight-Monodromy Conjecture
We will introduce the notion of perfectoid spaces. The theory can be seen as a kind of rigid geometry of infinite type, and the most important feature is that the theories over (deeply ramified extensions of) Q_p and over F_p((t)) are equivalent, generalizing to the relative situation a th
From playlist Peter SCHOLZE (oct 2011) - Perfectoid Spaces and the Weight-Monodromy Conjecture

Geordie Williamson 6 August 2020
Topic: Modular Representation Theory and Geometry Abstract: This will be a broad survey talk on interactions between geometry and representation theory, with a focus on representations in positive characteristic (“modular representation theory”). I will outline several basic questions (e.
From playlist Geordie Williamson external seminars

Theory of numbers: Gauss's lemma
This lecture is part of an online undergraduate course on the theory of numbers. We describe Gauss's lemma which gives a useful criterion for whether a number n is a quadratic residue of a prime p. We work it out explicitly for n = -1, 2 and 3, and as an application prove some cases of Di
From playlist Theory of numbers
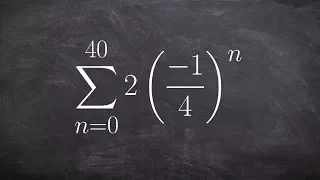
Learn to find the partial sum of a geometric sequence
👉 Learn how to find the geometric sum of a series. A series is the sum of the terms of a sequence. A geometric series is the sum of the terms of a geometric sequence. The formula for the sum of n terms of a geometric sequence is given by Sn = a[(r^n - 1)/(r - 1)], where a is the first term
From playlist Series

Damir Yeliussizov: "Bounds and inequalities for the Littlewood-Richardson coefficients"
Asymptotic Algebraic Combinatorics 2020 "Bounds and inequalities for the Littlewood-Richardson coefficients" Damir Yeliussizov - Kazakh-British Technical University Abstract: I will talk about various bounds, inequalities, and asymptotic estimates for the Littlewood-Richardson (LR) coeff
From playlist Asymptotic Algebraic Combinatorics 2020