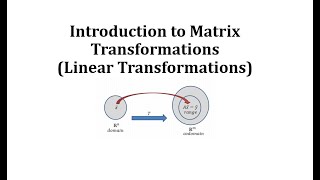
Matrix representation
Matrix representation is a method used by a computer language to store matrices of more than one dimension in memory.Fortran and C use different schemes for their native arrays. Fortran uses "Column Major", in which all the elements for a given column are stored contiguously in memory. C uses "Row Major", which stores all the elements for a given row contiguously in memory.LAPACK defines various matrix representations in memory. There is also Sparse matrix representation and Morton-order matrix representation.According to the documentation, in LAPACK the unitary matrix representation is optimized. Some languages such as Java store matrices using Iliffe vectors. These are particularly useful for storing irregular matrices. Matrices are of primary importance in linear algebra. (Wikipedia).