
Implications and Truth Conditions for Implications
This video defines an implication and when an implication is true or false.
From playlist Mathematical Statements (Discrete Math)

Implication and Biconditional Statements
The definition of implication and biconditional connectives along with some laws for working with them, plus the definition of tautology and contradiction. (In the part I got hung up on in the video, "p is necessary for q" can be read "p if q" (or "if q, then p"), and "p is sufficient fo
From playlist Linear Algebra

Causal Inference is a set of tools used to scientifically prove cause and effect, very commonly used in economics and medicine. This series will go over the basics that any data scientist should understand about causal inference - and point them to the tools they would need to perform it.
From playlist Causal Inference - The Science of Cause and Effect

From playlist e. Sets and Logic

Thanks so much for watching! Please comment below on what topics you'd like to see covered next!
From playlist Causal Inference - The Science of Cause and Effect

Assumptions - Causal Inference
In this video, I introduce the most important assumptions in casual inference that we use in order to avoid mistakes such as presuming association and causation to be one and the same, among others: - Positivity - SUTVA - Large Sample Size - Double Blinded - No Measurement Error - Exchan
From playlist Causal Inference - The Science of Cause and Effect

Logical Arguments, Formal Implication, and Laws of Inference [Discrete Math Class]
This video is not like my normal uploads. This is a supplemental video from one of my courses that I made in case students had to quarantine. this is a follow up to previous videos introducing propositional logic (mathematical propositions; logical connectives - "and", "or", "not" , the co
From playlist Discrete Mathematics Course
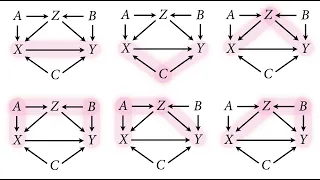
Statistical Rethinking 2022 Lecture 06 - Good & Bad Controls
Slides and other course materials: https://github.com/rmcelreath/stat_rethinking_2022 Intro video: https://www.youtube.com/watch?v=6erBpdV-fi0 Intro music: https://www.youtube.com/watch?v=Pc0AhpjbV58 Chapters: 00:00 Introduction 01:23 Parent collider 08:13 DAG thinking 27:48 Backdoor cri
From playlist Statistical Rethinking 2022

Fundamental Question - Causal Inference
In this video, I define the fundamental question and problem of causal inference and use an example to further explain the concept.
From playlist Causal Inference - The Science of Cause and Effect

Ideal Experiment - Causal Inference
In this video, I give you more details about the fundamental question and the fundamental problem of causal inference with the help of an example (our ideal experiment).
From playlist Causal Inference - The Science of Cause and Effect

Statistical Rethinking Fall 2017 - week10 lecture18 (fix)
Week 10, lecture 18 for Statistical Rethinking: A Bayesian Course with Examples in R and Stan, taught at MPI-EVA in Fall 2017. This lecture covers Chapters 14. Slides are available here: https://speakerdeck.com/rmcelreath/statistical-rethinking-fall-2017-lecture-18 Additional informati
From playlist Statistical Rethinking Fall 2017

Undertale Propositional Logic (#SoME2)
I'm sorry I had to do it because of the memes. Crash course educational look of propositional logic with the motivation to show how to prove things through proof by contradiction and proof by contraposition. Honorable shoutouts to @blackpenredpen and @drpeyam. God bless Toby Fox! Timel
From playlist Summer of Math Exposition 2 videos

Knowledge - Lecture 1 - CS50's Introduction to Artificial Intelligence with Python 2020
00:00:00 - Introduction 00:00:15 - Knowledge 00:04:52 - Propositional Logic 00:21:47 - Inference 00:40:06 - Knowledge Engineering 01:04:33 - Inference Rules 01:30:31 - Resolution 01:38:25 - First-Order Logic This course explores the concepts and algorithms at the foundation of modern arti
From playlist CS50's Introduction to Artificial Intelligence with Python 2020

Logic 6 - Propositional Resolutions | Stanford CS221: AI (Autumn 2021)
For more information about Stanford's Artificial Intelligence professional and graduate programs visit: https://stanford.io/ai Associate Professor Percy Liang Associate Professor of Computer Science and Statistics (courtesy) https://profiles.stanford.edu/percy-liang Assistant Professor
From playlist Stanford CS221: Artificial Intelligence: Principles and Techniques | Autumn 2021

Gödel's Incompleteness Theorems: An Informal Introduction to Formal Logic #SoME2
My entry into SoME2. Also, my first ever video. I hope you enjoy. The Book List: Logic by Paul Tomassi A very good first textbook. Quite slow at first and its treatment of first-order logic leaves a little to be desired in my opinion, but very good on context, i.e. why formal logic is im
From playlist Summer of Math Exposition 2 videos

Basic Methods: We define theorems and describe how to formally construct a proof. We note further rules of inference and show how the logical equivalence of reductio ad absurdum allows proof by contradiction.
From playlist Math Major Basics

Boolean Algebra Basics | Nathan Dalaklis
Boolean Algebra is one of the most fundamental concepts in theoretical mathematics, logic and philosophy. In this video I go through some of the basic operators, what a material implication is, and try to explain what vacuous truth is :D. _____________________ Last video: https://youtu.be/
From playlist The New CHALKboard

Logic 1 - Propositional Logic | Stanford CS221: AI (Autumn 2019)
For more information about Stanford’s Artificial Intelligence professional and graduate programs, visit: https://stanford.io/3ChWesU Topics: Logic Percy Liang, Associate Professor & Dorsa Sadigh, Assistant Professor - Stanford University http://onlinehub.stanford.edu/ Associate Professor
From playlist Stanford CS221: Artificial Intelligence: Principles and Techniques | Autumn 2019

Logically Equivalent Statements: Draw a Conclusion from a False Implication
This video explains how to determine what is true from a known false implication. mathispower4u.com
From playlist Symbolic Logic and Proofs (Discrete Math)
