
(PP 6.9) Conditional distributions of a Gaussian
For any subset of the coordinates of a multivariate Gaussian, the conditional distribution (given the remaining coordinates) is multivariate Gaussian.
From playlist Probability Theory

David Sutter: "A chain rule for the quantum relative entropy"
Entropy Inequalities, Quantum Information and Quantum Physics 2021 "A chain rule for the quantum relative entropy" David Sutter - IBM Zürich Research Laboratory Abstract: The chain rule for the conditional entropy allows us to view the conditional entropy of a large composite system as a
From playlist Entropy Inequalities, Quantum Information and Quantum Physics 2021
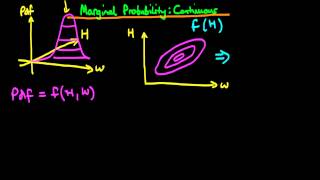
1 - Marginal probability for continuous variables
This explains what is meant by a marginal probability for continuous random variables, how to calculate marginal probabilities and the graphical intuition behind the method. If you are interested in seeing more of the material, arranged into a playlist, please visit: https://www.youtube.c
From playlist Bayesian statistics: a comprehensive course

What is a marginal probability?
An introduction to the concept of marginal probabilities, via the use of a simple 2 dimensional discrete example. If you are interested in seeing more of the material, arranged into a playlist, please visit: https://www.youtube.com/playlist?list=PLFDbGp5YzjqXQ4oE4w9GVWdiokWB9gEpm For mo
From playlist Bayesian statistics: a comprehensive course

Dylan Possamaï: Principal Agent Modelling - lecture 1
CIRM HYBRID EVENT These lectures will consist in an overview of recent progresses made in contracting theory, using the so-called dynamic programming approach. The basic situation is that of a Principal wanting to hire an Agent to do a task on his behalf, and who has to be properly incenti
From playlist Probability and Statistics

Xiaolu Tan: On the martingale optimal transport duality in the Skorokhod space
We study a martingale optimal transport problem in the Skorokhod space of cadlag paths, under finitely or infinitely many marginals constraint. To establish a general duality result, we utilize a Wasserstein type topology on the space of measures on the real value space, and the S-topology
From playlist HIM Lectures 2015

Determining the truth of a conditional statement
👉 Learn how to determine the truth or false of a conditional statement. A conditional statement is an if-then statement connecting a hypothesis (p) and the conclusion (q). If the hypothesis of a statement is represented by p and the conclusion is represented by q, then the conditional stat
From playlist Conditional Statements

What is a conditional probability?
An introduction to the concept of conditional probabilities via a simple 2 dimensional discrete example. If you are interested in seeing more of the material, arranged into a playlist, please visit: https://www.youtube.com/playlist?list=PLFDbGp5YzjqXQ4oE4w9GVWdiokWB9gEpm For more inform
From playlist Bayesian statistics: a comprehensive course

Write a statement in conditional form and determine the truth ex 2
👉 Learn how to determine the truth or false of a conditional statement. A conditional statement is an if-then statement connecting a hypothesis (p) and the conclusion (q). If the hypothesis of a statement is represented by p and the conclusion is represented by q, then the conditional stat
From playlist Conditional Statements

How to determine the truth table from a statement and determine its validity
👉 Learn how to determine the truth or false of a conditional statement. A conditional statement is an if-then statement connecting a hypothesis (p) and the conclusion (q). If the hypothesis of a statement is represented by p and the conclusion is represented by q, then the conditional stat
From playlist Conditional Statements

Peter Pivovarov: Random s-concave functions and isoperimetry
I will discuss stochastic geometry of s-concave functions. In particular, I will explain how a ”local” stochastic isoperimetry underlies several functional inequalities. A new ingredient is a notion of shadow systems for s-concave functions. Based on joint works with J. Rebollo Bueno.
From playlist Workshop: High dimensional spatial random systems

Large deviations of Markov processes (Part 2) by Hugo Touchette
Large deviation theory in statistical physics: Recent advances and future challenges DATE: 14 August 2017 to 13 October 2017 VENUE: Madhava Lecture Hall, ICTS, Bengaluru Large deviation theory made its way into statistical physics as a mathematical framework for studying equilibrium syst
From playlist Large deviation theory in statistical physics: Recent advances and future challenges

Large deviations of Markov processes (Part - 1) by Hugo Touchette
Large deviation theory in statistical physics: Recent advances and future challenges DATE: 14 August 2017 to 13 October 2017 VENUE: Madhava Lecture Hall, ICTS, Bengaluru Large deviation theory made its way into statistical physics as a mathematical framework for studying equilibrium syst
From playlist Large deviation theory in statistical physics: Recent advances and future challenges

Twenty third SIAM Activity Group on FME Virtual Talk Series
Date: Thursday, December 2, 2021, 1PM-2PM ET Speaker 1: Renyuan Xu, University of Southern California Speaker 2: Philippe Casgrain, ETH Zurich and Princeton University Moderator: Ronnie Sircar, Princeton Universit Join us for a series of online talks on topics related to mathematical fina
From playlist SIAM Activity Group on FME Virtual Talk Series

Determining the conditional probability from a contingency table
👉 Learn how to find the conditional probability of an event. Probability is the chance of an event occurring or not occurring. The probability of an event is given by the number of outcomes divided by the total possible outcomes. Conditional probability is the chance of an event occurring
From playlist Probability

Raúl Tempone: Multilevel and Multi-index Monte Carlo methods for the McKean-Vlasov equation
Abstract: We describe and analyze the Multi-Index Monte Carlo (MIMC) and the Multi-Index Stochastic Collocation (MISC) method for computing statistics of the solution of a PDE with random data. MIMC is both a stochastic version of the combination technique introduced by Zenger, Griebel and
From playlist Probability and Statistics

Modern finance and Macroeconomics: connecting various threads by Srinivas Raghavendra
Modern Finance and Macroeconomics: A Multidisciplinary Approach URL: http://www.icts.res.in/program/memf2015 DESCRIPTION: The financial meltdown of 2008 in the US stock markets and the subsequent protracted recession in the Western economies have accentuated the need to understand the dy
From playlist Modern Finance and Macroeconomics: A Multidisciplinary Approach

Yanghui Liu (Baruch College) -- Numerical approximations for rough differential equations
The rough paths theory provides a general framework for stochastic differential equations driven by processes with very low regularities, which has important applications in finance, statistical mechanics, hydro-dynamics and so on. The numerical approximation is a crucial step while applyi
From playlist Columbia SPDE Seminar

Jim Nolen: "A free boundary problem from Brownian bees in the infinite swarm limit in R^d"
High Dimensional Hamilton-Jacobi PDEs 2020 Workshop IV: Stochastic Analysis Related to Hamilton-Jacobi PDEs "A free boundary problem from Brownian bees in the infinite swarm limit in R^d" Jim Nolen - Duke University Abstract: I will discuss a stochastic interacting particle system in R^d
From playlist High Dimensional Hamilton-Jacobi PDEs 2020

How to determine the contrapositive of a conditional statement
👉 Learn how to find the contrapositive of a statement. The contrapositive of a statement is the switching of the hypothesis and the conclusion of a conditional statement and negating both. If the hypothesis of a statement is represented by p and the conclusion is represented by q, then the
From playlist Contrapositive of a Statement