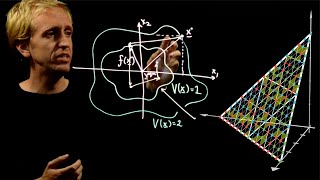
Lyapunov Stability via Sperner's Lemma
We go on whistle stop tour of one of the most fundamental tools from control theory: the Lyapunov function. But with a twist from combinatorics and topology. For more on Sperner's Lemma, including a simple derivation, please see the following wonderful video, which was my main source of i
From playlist Summer of Math Exposition Youtube Videos

Mod-06 Lec-35 Lyapunov Function Continued
Ordinary Differential Equations and Applications by A. K. Nandakumaran,P. S. Datti & Raju K. George,Department of Mathematics,IISc Bangalore.For more details on NPTEL visit http://nptel.ac.in.
From playlist IISc Bangalore: Ordinary Differential Equations and Applications | CosmoLearning.org Mathematics

Amir Ali Ahmadi, Princeton University
January 31, Amir Ali Ahmadi, Princeton University Two Problems at the Interface of Optimization and Dynamical Systems We propose and/or analyze semidefinite programming-based algorithms for two problems at the interface of optimization and dynamical systems: In part (i), we study the po
From playlist Spring 2020 Kolchin Seminar in Differential Algebra

Stability of Linear Dynamical Systems | The Practical Guide to Semidefinite Programming (3/4)
Third video of the Semidefinite Programming series. In this video, we will see how to use semidefinite programming to check whether a linear dynamical system is asymptotically stable. Thanks to Lyapunov's theory, this task can be reduced to searching for a so-called Lyapunov function. Pyth
From playlist Semidefinite Programming

Algorithmic Lie Symmetry Analysis and Group Classification for Ordinary Differential Equations
From playlist Spring 2018

Maxim Kontsevich, Equations for stability
Maxim Kontsevich, IHÉS, France Equations for stability
From playlist Conférence en l'honneur de Jean-Pierre Bourguignon

Particles starting near positive-time LCS attract onto negative-time LCS (zoom out)
This video depicts particles that start near the positive-time Lagrangian coherent structure (LCS) attract onto negative-time LCS as they are integrated forward in time. The flow field corresponds to a pitching flat plate at low Reynolds number (Re=100). This movie corresponds to Fig. 11
From playlist Finite-time Lyapunov exponents

Particles starting near positive-time LCS attract onto negative-time LCS
This video depicts particles that start near the positive-time Lagrangian coherent structure (LCS) attract onto negative-time LCS as they are integrated forward in time. The flow field corresponds to a pitching flat plate at low Reynolds number (Re=100). This movie corresponds to Fig. 11
From playlist Finite-time Lyapunov exponents

Lyapunov's Fractal (that Lyapunov knew nothing about) #SoME2
Hi everyone! I hope you enjoy my first video. I've known about Markus-Lyapunov Fractals for a few years now, and it surprised me that I couldn't find any video explaining how they work - so I thought I'd take a stab at it myself! This is also my submission for Summer of Math Exposition 2.
From playlist Summer of Math Exposition 2 videos

Aaron Ames: "Safety-Critical Control of Autonomous Systems"
Mathematical Challenges and Opportunities for Autonomous Vehicles 2020 Workshop II: Safe Operation of Connected and Autonomous Vehicle Fleets "Safety-Critical Control of Autonomous Systems" Aaron Ames - California Institute of Technology Abstract: Guaranteeing safe behavior is a critical
From playlist Mathematical Challenges and Opportunities for Autonomous Vehicles 2020

Large coupling asymptotics for the Lyapunov...with analytic potentials -Christoph Marx
Analysis Math-Physics Seminar Topic: Reinforced random walks and statistical physics Speaker: Christoph Marx Affiliation: Oberlin College Date: Wednesday, January 25 For more video, visit http://video.ias.edu
From playlist Mathematics

Machine learning analysis of chaos and vice versa - Edward Ott, University of Maryland
About the talk In this talk we first consider the situation where one is interested in gaining understanding of general dynamical properties of a chaotically time evolving system solely through access to time series measurements that depend on the evolving state of an, otherwise unknown,
From playlist Turing Seminars

Lyapunov exponents, from the 1960's to the 2020's by Marcelo Viana
DISTINGUISHED LECTURES LYAPUNOV EXPONENTS, FROM THE 1960'S TO THE 2020'S SPEAKER: Marcelo Viana (IMPA, Brazil) DATE: 24 September 2019, 16:00 to 17:30 VENUE: Ramanujan Lecture Hall The ergodic theory of Lyapunov exponents, initiated by the work of Furstenberg and Kesten at the dawn of
From playlist DISTINGUISHED LECTURES

Mod-06 Lec-34 Lyapunov Function
Ordinary Differential Equations and Applications by A. K. Nandakumaran,P. S. Datti & Raju K. George,Department of Mathematics,IISc Bangalore.For more details on NPTEL visit http://nptel.ac.in.
From playlist IISc Bangalore: Ordinary Differential Equations and Applications | CosmoLearning.org Mathematics

Stanford Seminar - Model Predictive Control of Hybrid Dynamical Systems
Ricardo Sanfelice UC Santa Cruz November 8, 2019 Hybrid systems model the behavior of dynamical systems in which the states can evolve continuously and, at isolate time instances, exhibit instantaneous jumps. Such systems arise when control algorithms that involve digital devices are appl
From playlist Stanford AA289 - Robotics and Autonomous Systems Seminar

Charles Favre: Explosion of Lyapunov exponents using non-Archimedean geometry
Abstract: We consider a meromorphic family of endomorphisms of the complex projective space parameterized by the unit disk, and show that the blow-up of the Lyapunov exponent near the origin is controlled by a non-Archimedean quantity. Recording during the thematic meeting : "p-adic Analy
From playlist Algebraic and Complex Geometry

Peter Benner: Matrix Equations and Model Reduction, Lecture 5
Peter Benner from the Max Planck Institute presents: Matrix Equations and Model Reduction; Lecture 5
From playlist Gene Golub SIAM Summer School Videos