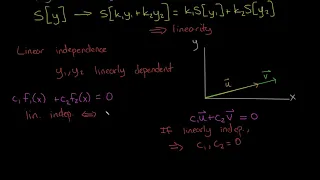
Differential Equations: Linear Independence
Linear independence is a core idea from Linear Algebra. Surprisingly, it's also important in differential equations. This video is the second precursor to our discussion of homogeneous differential equations.
From playlist Differential Equations

Further examination of independence
From playlist Unit 5 Probability A: Basic Probability

A02 Independence of the solution set
The independence of a linear system. How to make sure that a set of solutions are not constant multiples of each other.
From playlist A Second Course in Differential Equations

More Help with Independence Part 2Indep FE pt 2
More insight into the probability concept of independence
From playlist Unit 5 Probability A: Basic Probability

Math 060 092717 Linear Independence
Linear independence: definition of, examples and non-examples; intuition (dependence is redundancy; independence is minimality). Equivalence of dependence and a vector being included in the span of the others. Equivalence of independence with every vector in the span being uniquely expre
From playlist Course 4: Linear Algebra (Fall 2017)

MIT RES.6-012 Introduction to Probability, Spring 2018 View the complete course: https://ocw.mit.edu/RES-6-012S18 Instructor: John Tsitsiklis License: Creative Commons BY-NC-SA More information at https://ocw.mit.edu/terms More courses at https://ocw.mit.edu
From playlist MIT RES.6-012 Introduction to Probability, Spring 2018

(0:00) Independence of two events (4:12) (Mutual) Independence of multiple events (9:30) Conditional Independence of two events A playlist of the Probability Primer series is available here: http://www.youtube.com/view_play_list?p=17567A1A3F5DB5E4
From playlist Probability Theory
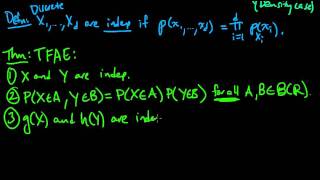
(PP 5.4) Independence, Covariance, and Correlation
(0:00) Definition of independent random variables. (5:10) Characterizations of independence. (10:54) Definition of covariance. (13:10) Definition of correlation. A playlist of the Probability Primer series is available here: http://www.youtube.com/view_play_list?p=17567A1A3F5DB5E4
From playlist Probability Theory
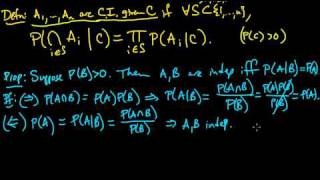
(PP 2.3) Independence (continued)
(0:00) (Mutual) Independence of an infinite sequence of events. (1:55) Conditional Independence of multiple events. (3:28) Relationship between independence and conditional probability. (7:23) Example illustrating the relationships between independence, pairwise independence, mutu
From playlist Probability Theory

W. Zheng - Compatible systems along the boundary
A theorem of Deligne says that compatible systems of l-adic sheaves on a smooth curve over a finite field are compatible along the boundary. I will present an extension of Deligne's theorem to schemes of finite type over the ring of integers of a local field, based on Gabber's theorem on c
From playlist Arithmetic and Algebraic Geometry: A conference in honor of Ofer Gabber on the occasion of his 60th birthday

Spectral Independence in High-dimensional Expanders and Applications... - Kuikui Liu
Computer Science/Discrete Mathematics Seminar II Topic: Spectral Independence in High-dimensional Expanders and Applications to the Hardcore Model Speaker: Kuikui Liu Affiliation: University of Washington Date: February 27, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Sylvie Paycha: A Galois group on meromorphic germs and locality evaluators
Talk by Sylvie Paycha in Global Noncommutative Geometry Seminar (Europe) http://www.noncommutativegeometry.nl/ncgseminar/ on February 9, 2021
From playlist Global Noncommutative Geometry Seminar (Europe)
Sylvie PAYCHA - From Complementations on Lattices to Locality
A complementation proves useful to separate divergent terms from convergent terms. Hence the relevance of complementation in the context of renormalisation. The very notion of separation is furthermore related to that of locality. We extend the correspondence between Euclidean structures o
From playlist Algebraic Structures in Perturbative Quantum Field Theory: a conference in honour of Dirk Kreimer's 60th birthday

Progress on algorithmic versions of the Lovasz Local Lemma - Aravind Srinivasan
Aravind Srinivasan University of Maryland, College Park April 7, 2014 There has been substantial progress on algorithmic versions and generalizations of the Lovasz Local Lemma recently, with some of the main ideas getting simplified as well. I will survey some of the main ideas of Moser &
From playlist Mathematics

The measurement problem and some mild solutions by Dustin Lazarovici (Lecture - 04)
21 November 2016 to 10 December 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore Quantum Theory has passed all experimental tests, with impressive accuracy. It applies to light and matter from the smallest scales so far explored, up to the mesoscopic scale. It is also a necessary ingredie
From playlist Fundamental Problems of Quantum Physics

Rasch measurement unidimensionality and local independence (Part 2)
Unidimensionality and Local Independence in Rasch measurement - Part 2 Please see: https://journals.sagepub.com/doi/pdf/10.1177/0265532220927487 Note: Unidimensionality and local independence are also requirements of other similar techniques such as unidimensional IRT modeling. There ar
From playlist Rasch Measurement

Independence of ℓℓ and local terms - Martin Olsson
Martin Olsson University of California, Berkeley November 14, 2013 Let kk be an algebraically closed field and let c:C→X×Xc:C→X×X be a correspondence. Let ℓℓ be a prime invertible in kk and let K∈Dbc(X,ℚ⎯⎯⎯⎯⎯ℓ)K∈Dcb(X,Q¯ℓ) be a complex. An action of cc on KK is by definition a map u:c∗1K→c
From playlist Mathematics

Optimal Mixing of Glauber Dynamics: Entropy Factorization via High-Dimensional Expan - Zongchen Chen
Computer Science/Discrete Mathematics Seminar I Topic: Optimal Mixing of Glauber Dynamics: Entropy Factorization via High-Dimensional Expansion Speaker: Zongchen Chen Affiliation: Georgia Institute of Technology Date: February 22, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

Deep InfoMax: Learning deep representations by mutual information estimation and maximization | AISC
For more details including paper and slides, visit https://aisc.a-i.science/events/2019-04-11/ Discussion lead/coauthor: Karan Grewal Abstract Building agents to interact with the web would allow for significant improvements in knowledge understanding and representation learning. Howev
From playlist Natural Language Processing

Linear Independence Problems - Using the Definition
In this video, I review the definition of linear independence and work through some practice problems using the definition. To learn more about linear independence, check out this lecture in my Linear Algebra Lectures video series: https://youtu.be/KE7xHcwfxzQ
From playlist Linear Algebra Lectures