
Photoelectric Effect History: A Battle of Einstein vs. Lenard
Einstein won his Nobel Prize for the photoelectric effect, but why? He was more famous for relativity. It all has to do with a man named Philipp Lenard. Lenard's experiments inspired Einstein, and Lenard at first befriended Einstein but then turned and made his life a misery. This is a
From playlist Early History of Quantum Mechanics

Photoelectric Effect History: Einstein vs. Lenard
Einstein won his Nobel Prize for the photoelectric effect, but why? He was more famous for relativity. It all has to do with a man named Philipp Lenard. Lenard's experiments inspired Einstein, and Lenard at first befriended Einstein but then turned and made his life a misery. This is a
From playlist Nobel Prize History

Andrew Lobb: Quantum sln knot cohomology and the slice genus
Abstract: We will give an overview of the information about the smooth slice genus so far yielded by the quantum 𝔰𝔩n knot cohomologies. Recording during the thematic meeting "Knotted Embeddings in Dimensions 3 and 4" the February 15, 2017 at the Centre International de Rencontres Mathémat
From playlist Topology

Conversion Arcs and 2,916,485,648,612,232,232,816 (MegaFavNumbers)
I'm sorry. The MegaFavNumbers playlist: https://www.youtube.com/playlist?list=PLar4u0v66vIodqt3KSZPsYyuULD5meoAo
From playlist MegaFavNumbers

The dynamics of regularized flows on convex bodies -James Lee
Optimization, Complexity and Invariant Theory Topic: The dynamics of regularized flows on convex bodies Speaker: James Lee Affiliation: University of Washington Date: June 7. 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

27c3: Friede sei mit Euren Daten
Speaker: Jochim Selzer A data-protection law in a church outing Parelleluniversum German Federal Data Protection and church lead a parallel existence. While the Federal Privacy Act is perceived by the public and critical eye, the least is at all clear that there is also a detached BDSG o
From playlist 27C3: We come in peace

#MegaFavNumbers: 10,904,493,600 & Fibonacci Numbers
This is my #MegaFavNumber. Link to all the #MegaFavNumbers Videos: https://www.youtube.com/watch?v=R2eQVqdUQLI&list=PLar4u0v66vIodqt3KSZPsYyuULD5meoAo Channel Links: Website: https://sites.google.com/view/pentamath Channel: https://www.youtube.com/channel/UCervsuIC9pv4eQq98hAgOZA Subscri
From playlist MegaFavNumbers

#MegaFavNumbers - 7,588,043,387,109,376 by Egi
87,109,376^2=7,588,043,387,109,376. The last 8 digits is the square root😀, it's called an automorphic number which n^2 ends with n
From playlist MegaFavNumbers
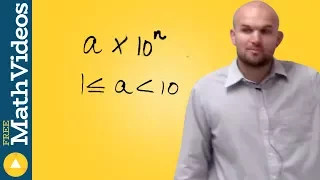
What is the definition of scientific notation
👉 Learn about scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is the number of digits up to t
From playlist Scientific Notation | Learn About

What are Irrational Numbers? | Number System | Don't Memorise
Watch this video to know more about Rational numbers, Irrational Numbers, Real Numbers and Number System. To learn more about Irrational Numbers, enroll in our full course now: https://infinitylearn.com/microcourses?utm_source=youtube&utm_medium=Soical&utm_campaign=DM&utm_content=CtRtXoT_
From playlist Irrational Numbers

My own choice for a number over 1,000,000 is this 617 digit boy: 251959084756578934940271832400483985714292821262040320277771378360436620207075955562640185258807844069182906412495150821892985591491761845028084891200728449926873928072877767359714183472702618963750149718246911650776133798590
From playlist MegaFavNumbers

MegaFavNumbers | 8.07x10^67 vs. 137,327,459,106,673,000,000,000,000,000,000,000,000,000,000,000,000
This video compares the number of ways to shuffle a deck of cards to the number of atoms on Earth. #MegaFavNumbers 80,658,175,170,943,878,571,660,636,856,403,766,975,289,505,440,883,277,824,000,000,000,000 vs 137,327,459,106,673,000,000,000,000,000,000,000,000,000,000,000,000.00
From playlist MegaFavNumbers

There are a lot more numbers than I thought there were - MegaFavNumbers
A short video detailing my favorite number larger than 1 million! There are so many numbers out there it was hard to choose from, but I’m glad I could participate in the #MegaFavNumbers series
From playlist MegaFavNumbers

How is i equal to square root of -1?
What is 'i'? More importantly, what is a complex number? How are complex numbers relevant to the context of other familiar numbers? Chapters: 00:00 Introduction 01:46 Logo of Reals and Rationals 02:11 Expanding real numbers 03:25 Motivation using whole (natural) numbers 06:08 Planar numb
From playlist Summer of Math Exposition 2 videos

Fun with Math: Surprises with Arithmetic and Numbers
Stephen Wolfram shows kids and adults some fun unique things you can do with math. All demonstrations powered by the Wolfram Language. Originally livestreamed at: https://twitch.tv/stephen_wolfram Follow us on our official social media channels: Twitter: https://twitter.com/WolframRese
From playlist Stephen Wolfram Livestreams

How to understand the REAL NUMBER LINE - COLLEGE ALGEBRA
In this video we talk about natural numbers, whole numbers, integers, rational numbers, irrational numbers, and real numbers. We also show the real number line and the inequalities less than and greater than. 00:00 Intro 00:29 Number system 04:53 Visual representation of numbers 07:37 Rea
From playlist College Algebra

This video provides a basic introduction into real numbers. It explains how to distinguish them from imaginary numbers. It also discusses the difference between rational and irrational numbers as well as integers, natural numbers, and whole numbers. Examples include repeating and non-re
From playlist New Algebra Playlist

This chemistry video tutorial answers the question - what are isotopes? Isotopes are substances that are composed of the same element but consist of different mass numbers and number of neutrons. They share the same atomic number and therefore the same number of protons. This video cont
From playlist New AP & General Chemistry Video Playlist

Is your name also a NUMBER? | Find what number your name is with math and code
In base-36, the number 360927794919225 is expressed using the numeral deeplizard. Yes. Everyone's name is also a number in some base. Let's check this out. Notebook links: https://beta.observablehq.com/@deeplizard/positional-numeral-systems https://beta.observablehq.com/@deeplizard/find-
From playlist Data Science - Learn to code for beginners
