
Verifying Trigonometric Identities: The Fundamental Identities
Visit http://mathispower4u.wordpress.com/ for a categorized and searchable list of all videos.
From playlist Reciprocal, Quotient, Negative, and Pythagorean Trigonometric Identities

Trigonometric Identities (1 of 3: Reciprocals, Ratios & Complements)
More resources available at www.misterwootube.com
From playlist Trigonometric Functions and Identities
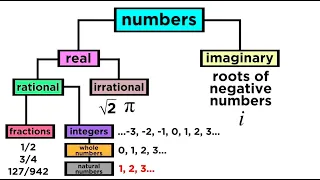
What are the Types of Numbers? Real vs. Imaginary, Rational vs. Irrational
We've mentioned in passing some different ways to classify numbers, like rational, irrational, real, imaginary, integers, fractions, and more. If this is confusing, then take a look at this handy-dandy guide to the taxonomy of numbers! It turns out we can use a hierarchical scheme just lik
From playlist Algebra 1 & 2

Trig identities - What are they?
► My Trigonometry course: https://www.kristakingmath.com/trigonometry-course Trig identities are pretty tough for most people, because 1) there are so many of them, and 2) they’re hard to remember, and 3) it’s tough to recognize when you’re supposed to use them! But don’t worry, because
From playlist Trigonometry

Intro to Trigonometric Identities - part 1
In this video I go through a brief introduction to trig identities. I look at well known identities such as sin^x + cos^x = 1, then go through some example problems. Part 2: https://youtu.be/w8whFeSccX0 practice problems: http://bit.ly/2ITWDYL Support the channel: https://www.youtube.com
From playlist Trigonometry - A-level/year 12

Fundamental Trigonometric Identities: Reciprocal, Quotient, and Pythagorean Identities
Visit http://mathispower4u.wordpress.com/ for a categorized and searchable list of all videos.
From playlist Reciprocal, Quotient, Negative, and Pythagorean Trigonometric Identities

What do I need to know to verify trigonometric Identities
👉 Learn all about the different trigonometric identities and how they can be used to evaluate, verify, simplify and solve trigonometric equations. The identities discussed in this playlist will involve the quotient, reciprocal, half-angle, double angle, Pythagorean, sum, and difference. I
From playlist Learn About Trigonometric Identities

Understand where even and odd identities come from
👉 Learn all about the different trigonometric identities and how they can be used to evaluate, verify, simplify and solve trigonometric equations. The identities discussed in this playlist will involve the quotient, reciprocal, half-angle, double angle, Pythagorean, sum, and difference. I
From playlist Learn About Trigonometric Identities

What are your three basic fundamental trigonometric identities
👉 Learn all about the different trigonometric identities and how they can be used to evaluate, verify, simplify and solve trigonometric equations. The identities discussed in this playlist will involve the quotient, reciprocal, half-angle, double angle, Pythagorean, sum, and difference. I
From playlist Learn About Trigonometric Identities

Transposes and Inverses II | Linear Algebra MATH1141 | N J Wildberger
We introduce the notion of the inverse of an n by n matrix. Concrete formulas for the 1 by 1 and the 2 by 2 cases are given, and we derive various useful properties. ************************ Screenshot PDFs for my videos are available at the website http://wildegg.com. These give you a co
From playlist Higher Linear Algebra

Algebraic identities | Arithmetic and Geometry Math Foundations 53 | N J Wildberger
Algebraic identities are at the heart of a lot of mathematics, especially geometry and analysis. Here we have a look at some simple and familiar identities, such as the difference of squares, the geometric series, and identities that go back to Pythagoras and Fibonacci. This lecture is pa
From playlist Math Foundations

The algebra of nxn matrices | Linear Algebra MATH1141 | N J Wildberger
We introduce the algebra of n by n matrices, concentrating on the 2 by 2 case. The zero and identity matrices are discussed, along with some special types. And we see how this is all a big extension of ordinary arithmetic. ************************ Screenshot PDFs for my videos are availab
From playlist Higher Linear Algebra

The Binomial Chu Vandermonde Identity: a new unification? | Algebraic Calculus Two | Wild Egg Maths
We suggest a novel unification of the Binomial and Chu Vandermonde identities, leading to an unusual introduction of the exponential polyseries, along with Newton's reciprocal polyseries. The main idea is to introduce a generalization of Knuth's rising and falling powers notation, which w
From playlist Algebraic Calculus Two

Trig identities and the exponential | Linear Algebra MATH1141 | N J Wildberger
Many trigonometric identities, for example double angle formulas, are easily proved using the complex exponential. But in fact we can use this to get a lot more identities. Here we also meet the Chebyshev polynomials, see some nice algebraic tricks for simplifying binomial expansions, and
From playlist Higher Linear Algebra

Logic Identities via the Algebra of Boole | MathFoundations 276 | N J Wildberger
We show how lots logic identities can be quickly derived using the Algebra of Boole. These include the standard beginning laws of Boolean algebra, such as the associative, commutative and distributive laws, also the laws of absorption and identity and de Morgan's laws. But also the Conditi
From playlist Boole's Logic and Circuit Analysis

The Chu Vandermonde Identity | Algebraic Calculus Two | Wild Egg Maths
We introduce the Chu Vandermonde identity as a key ingredient in establishing Newton's polyseries theorem, which gives the fundamental multiplicative relation between the various extensions of the Binomial theorem that Newton discovered for rational powers. Along the way we look at the as
From playlist Algebraic Calculus Two

The S3 character table - a (somewhat) new meaning | Diffusion Symmetry 2 | N J Wildberger
With diffusion symmetry, we explore mathematical objects or physical systems by spreading or diffusing from an initial point. The algebraic objects that result are hypergroups, or fusion algebra, or one of many similar and almost equivalent systems found in combinatorics, group theory, num
From playlist Diffusion Symmetry: A bridge between mathematics and physics

Invertible matrices and systems of linear equations II | Linear Algebra MATH1141 | N J Wildberger
We continue showing that an n by n matrix is invertible precisely when the equation Ax=b has a unique solution for any b. Along the way we will need to look at the matrix formulation of elementary row operations, and how these elementary matrices are invertible. This is a rather subtle but
From playlist Higher Linear Algebra

Compound Angle Identities (1 of 3: Proving sin(a+b) geometrically)
More resources available at www.misterwootube.com
From playlist Further Trigonometric Identities

Transposes and Inverses III | Linear Algebra MATH1141 | N J Wildberger
We continue the discussion on transposes and inverses, and how they interact. We also mention symmetric, skew-symmetric and orthogonal n by n matrices. ************************ Screenshot PDFs for my videos are available at the website http://wildegg.com. These give you a concise overview
From playlist Higher Linear Algebra