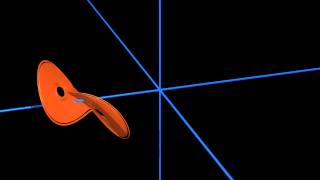
This video introduces chaotic dynamical systems, which exhibit sensitive dependence on initial conditions. These systems are ubiquitous in natural and engineering systems, from turbulent fluids to the motion of objects in the solar system. Here, we discuss how to recognize chaos and how
From playlist Engineering Math: Differential Equations and Dynamical Systems

Lyapunov's Fractal (that Lyapunov knew nothing about) #SoME2
Hi everyone! I hope you enjoy my first video. I've known about Markus-Lyapunov Fractals for a few years now, and it surprised me that I couldn't find any video explaining how they work - so I thought I'd take a stab at it myself! This is also my submission for Summer of Math Exposition 2.
From playlist Summer of Math Exposition 2 videos

Dynamics of piecewise smooth maps (Lecture - 01) by Paul Glendinning
PROGRAM DYNAMICS OF COMPLEX SYSTEMS 2018 ORGANIZERS Amit Apte, Soumitro Banerjee, Pranay Goel, Partha Guha, Neelima Gupte, Govindan Rangarajan and Somdatta Sinha DATE: 16 June 2018 to 30 June 2018 VENUE: Ramanujan hall for Summer School held from 16 - 25 June, 2018; Madhava hall for W
From playlist Dynamics of Complex systems 2018

Quantum chaos, random matrices and statistical physics (Lecture 03) by Arul Lakshminarayan
ORGANIZERS: Abhishek Dhar and Sanjib Sabhapandit DATE: 27 June 2018 to 13 July 2018 VENUE: Ramanujan Lecture Hall, ICTS Bangalore This advanced level school is the ninth in the series. This is a pedagogical school, aimed at bridging the gap between masters-level courses and topics in
From playlist Bangalore School on Statistical Physics - IX (2018)

Quantum-classical Correspondence in Chaotic PT-symmetric Systems by Eva-Maria Graefe
PROGRAM NON-HERMITIAN PHYSICS (ONLINE) ORGANIZERS: Manas Kulkarni (ICTS, India) and Bhabani Prasad Mandal (Banaras Hindu University, India) DATE: 22 March 2021 to 26 March 2021 VENUE: Online Non-Hermitian Systems / Open Quantum Systems are not only of fundamental interest in physics a
From playlist Non-Hermitian Physics (ONLINE)
DevOpsDays Boston 2017 - There is No Root Cause... by Matthew Boeckman
DevOpsDays Boston 2017 - There is No Root Cause: Emergent Behavior in Complex Systems by Matthew Boeckman What went wrong? Why does this always happen? How can we ensure it Never Happens Again? For most of the internet age, engineering teams have focused on finding a cause of an outage. A
From playlist DevOpsDays Boston 2017

Tiago Pereira - Ergodic basis pursuit induces robust network reconstruction - IPAM at UCLA
Recorded 29 August 2022. Tiago Pereira of the University of São Paulo (USP) presents "Ergodic basis pursuit induces robust network reconstruction" at IPAM's Reconstructing Network Dynamics from Data: Applications to Neuroscience and Beyond. Learn more online at: http://www.ipam.ucla.edu/pr
From playlist 2022 Reconstructing Network Dynamics from Data: Applications to Neuroscience and Beyond

Topics in Dynamical Systems: Fixed Points, Linearization, Invariant Manifolds, Bifurcations & Chaos
This video provides a high-level overview of dynamical systems, which describe the changing world around us. Topics include nonlinear dynamics, linearization at fixed points, eigenvalues and eigenvectors, bifurcations, invariant manifolds, and chaos!! @eigensteve on Twitter eigensteve.co
From playlist Dynamical Systems (with Machine Learning)

Products may be or become complicated for many reasons, and teams are often asked to make them “simpler and better.” How do we identify when and why something is complicated, and how can we make it simpler? David will talk about methods to make products and experiences simpler, some of the
From playlist Design

Corinna Ulcigrai - 1/6 Parabolic dynamics and renormalization: an introduction
Parabolic dynamical systems are mathematical models of the many phenomena which display a "slow" form of chaotic evolution, in the sense that nearby trajectories diverge polynomially in time. In contrast with hyperbolic and elliptic dynamical systems, there is no general theory which desc
From playlist Corinna Ulcigrai - Parabolic dynamics and renormalization: an introduction

Chaos9 La recherche aujourd'hui
From playlist Chaos français