
How to Determine if Functions are Linearly Independent or Dependent using the Definition
How to Determine if Functions are Linearly Independent or Dependent using the Definition If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Th
From playlist Zill DE 4.1 Preliminary Theory - Linear Equations

Every Subset of a Linearly Independent Set is also Linearly Independent Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys A proof that every subset of a linearly independent set is also linearly independent.
From playlist Proofs

Determining if a vector is a linear combination of other vectors
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Determining if a vector is a linear combination of other vectors
From playlist Linear Algebra
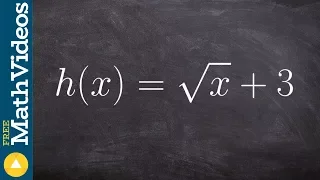
How to determine if an equation is a linear relation
👉 Learn how to determine if an equation is a linear equation. A linear equation is an equation whose highest exponent on its variable(s) is 1. The variables do not have negative or fractional, or exponents other than one. Variables must not be in the denominator of any rational term and c
From playlist Write Linear Equations

👉 Learn about graphing linear equations. A linear equation is an equation whose highest exponent on its variable(s) is 1. i.e. linear equations has no exponents on their variables. The graph of a linear equation is a straight line. To graph a linear equation, we identify two values (x-valu
From playlist ⚡️Graph Linear Equations | Learn About

Summary for graph an equation in Standard form
👉 Learn about graphing linear equations. A linear equation is an equation whose highest exponent on its variable(s) is 1. i.e. linear equations has no exponents on their variables. The graph of a linear equation is a straight line. To graph a linear equation, we identify two values (x-valu
From playlist ⚡️Graph Linear Equations | Learn About

When do you know if a relations is in linear standard form
👉 Learn how to determine if an equation is a linear equation. A linear equation is an equation whose highest exponent on its variable(s) is 1. The variables do not have negative or fractional, or exponents other than one. Variables must not be in the denominator of any rational term and c
From playlist Write Linear Equations

Review of Linear Time Invariant Systems
http://AllSignalProcessing.com for more great signal-processing content: ad-free videos, concept/screenshot files, quizzes, MATLAB and data files. Review: systems, linear systems, time invariant systems, impulse response and convolution, linear constant-coefficient difference equations
From playlist Introduction and Background

Linear differential equations: how to solve
Free ebook http://bookboon.com/en/learn-calculus-2-on-your-mobile-device-ebook How to solve linear differential equations. In mathematics, linear differential equations are differential equations having differential equation solutions which can be added together to form other solutions.
From playlist A second course in university calculus.

The quantum query complexity of sorting under (...) - J. Roland - Main Conference - CEB T3 2017
Jérémie Roland (Brussels) / 15.12.2017 Title: The quantum query complexity of sorting under partial information Abstract: Sorting by comparison is probably one of the most fundamental tasks in algorithmics: given $n$ distinct numbers $x_1,x_2,...,x_n$, the task is to sort them by perfor
From playlist 2017 - T3 - Analysis in Quantum Information Theory - CEB Trimester

Lecture 5: Differential Forms (Discrete Differential Geometry)
Full playlist: https://www.youtube.com/playlist?list=PL9_jI1bdZmz0hIrNCMQW1YmZysAiIYSSS For more information see http://geometry.cs.cmu.edu/ddg
From playlist Discrete Differential Geometry - CMU 15-458/858

Applied ML 2020 - 11 - Model Inspection and Feature Selection
Course materials at https://www.cs.columbia.edu/~amueller/comsw4995s20/schedule/
From playlist Applied Machine Learning 2020

17 Machine Learning: Artificial Neural Networks
Let's demystify artificial neural networks with an accessible lecture on artificial neural networks, including the architecture, parameters, hyperparameters, and training with back-propagation and steepest descent. A demonstration workflow is available at https://git.io/fjlao. Try out a
From playlist Machine Learning

CONFERENCE Recording during the thematic meeting : « ALgebraic and combinatorial methods for COding and CRYPTography» the February 20, 2023 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Jean Petit Find this video and other talks given by worldwid
From playlist Combinatorics

Sascha Husa (2) - Introduction to theory and numerics of partial differential equations
PROGRAM: NUMERICAL RELATIVITY DATES: Monday 10 Jun, 2013 - Friday 05 Jul, 2013 VENUE: ICTS-TIFR, IISc Campus, Bangalore DETAL Numerical relativity deals with solving Einstein's field equations using supercomputers. Numerical relativity is an essential tool for the accurate modeling of a wi
From playlist Numerical Relativity

Stanford CS224N: NLP with Deep Learning | Winter 2019 | Lecture 3 – Neural Networks
For more information about Stanford’s Artificial Intelligence professional and graduate programs, visit: https://stanford.io/3kzqrg1 Professor Christopher Manning Thomas M. Siebel Professor in Machine Learning, Professor of Linguistics and of Computer Science Director, Stanford Artificial
From playlist Stanford CS224N: Natural Language Processing with Deep Learning Course | Winter 2019

We propose a sparse regression method capable of discovering the governing partial differential equation(s) of a given system by time series measurements in the spatial domain. The regression framework relies on sparsity promoting techniques to select the nonlinear and partial derivative
From playlist Research Abstracts from Brunton Lab

Part IV: Matrix Algebra, Lec 4 | MIT Calculus Revisited: Multivariable Calculus
Part IV: Matrix Algebra, Lecture 4: Inverting More General Systems of Equations Instructor: Herbert Gross View the complete course: http://ocw.mit.edu/RES18-007F11 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT Calculus Revisited: Multivariable Calculus

ML Tutorial: Probabilistic Numerical Methods (Jon Cockayne)
Machine Learning Tutorial at Imperial College London: Probabilistic Numerical Methods Jon Cockayne (University of Warwick) February 22, 2017
From playlist Machine Learning Tutorials

Linear Dependence of {x^2-1, x^2+x, x+1} Using Wronskian
ODEs: Consider the set of functions S = {x^2-1, x^2+x, x+1}. Is S a linearly dependent set? If not, find a relation in S. We test linear independence by computing the Wronskian.
From playlist Differential Equations