
Séminaire Bourbaki 08/11/2014 - Aurélien Djament 2/4
" La propriété noethérienne pour les foncteurs entre espaces vectoriels " [d'après A. Putman, S. Sam et A. Snowden] Les bases de Gröbner permettent de démontrer le théorème de la base de Hilbert, en ramenant le caractère noethérien à une propriété combinatoire d'ensembles ordonnés. A. P
From playlist Bourbaki - 08 novembre 2014

Nonlinear algebra, Lecture 3: "Elimination and Implicitization", by Bernd Sturmfels
This is the third lecture in the IMPRS Ringvorlesung, the advanced graduate course at the Max Planck Institute for Mathematics in the Sciences.
From playlist IMPRS Ringvorlesung - Introduction to Nonlinear Algebra

Elisa Gorla: Complexity of Groebner bases computations and applications to cryptography - lecture 1
CIRM VIRTUAL EVENT Recorded during the meeting "French Computer Algebra Days" the March 02, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audio
From playlist Virtual Conference

Asymptotic spectra and their applications II - Jeroen Zuiddam
Computer Science/Discrete Mathematics Seminar II Topic: Asymptotic spectra and their applications II Speaker: Jeroen Zuiddam Affiliation: Member, School of Mathematics Date: October 16, 2018 For more video please visit http://video.ias.edu
From playlist Mathematics

How to quickly write out the unit circle
👉 Learn about the unit circle. A unit circle is a circle which radius is 1 and is centered at the origin in the cartesian coordinate system. To construct the unit circle we take note of the points where the unit circle intersects the x- and the y- axis. The points of intersection are (1, 0
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)

Infinite bridges for Rémy's algorithm
Distinguished Visitor Lecture Series Infinite bridges for Rémy's algorithm Steve Evans University of California at Berkeley, USA
From playlist Distinguished Visitors Lecture Series

Igor Kortchemski: Condensation in random trees - Lecture 3
We study a particular family of random trees which exhibit a condensation phenomenon (identified by Jonsson & Stefánsson in 2011), meaning that a unique vertex with macroscopic degree emerges. This falls into the more general framework of studying the geometric behavior of large random dis
From playlist Probability and Statistics

Learn how to construct the unit circle
👉 Learn about the unit circle. A unit circle is a circle which radius is 1 and is centered at the origin in the cartesian coordinate system. To construct the unit circle we take note of the points where the unit circle intersects the x- and the y- axis. The points of intersection are (1, 0
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)

Math 131 083116 Lecture #01 Ordered Sets and Boundedness
[Notes for the course and others may be downloaded at http://community.scrippscollege.edu/wcwou/online-resources/class-notes/.] Heading towards the real (and complex) numbers: problems with the rational numbers (algebraic incompleteness, analytic incompleteness). Square root of two is ir
From playlist Course 7: (Rudin's) Principles of Mathematical Analysis

Ulrich Bauer: Ripser Efficient computation of Vietoris–Rips persistence barcodes
The lecture was held within the framework of the Hausdorff Trimester Program : Applied and Computational Algebraic Topology
From playlist HIM Lectures: Special Program "Applied and Computational Algebraic Topology"

Oussama Hamza - Hilbert series and mild groups
Let $p$ be an odd prime number and $G$ a finitely generated pro-$p$ group. Define $I(G)$ the augmentation ideal of the group algebra of $G$ over $F_p$ and define the Hilbert series of $G$ by: $G(t):=sum_{n\in \NN} \dim_{\F_p} I^n(G)/I^{n+1}(G)$.The series $G(t)$ gives several information
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory

Alexander HULPKE - Computational group theory, cohomology of groups and topological methods 5
The lecture series will give an introduction to the computer algebra system GAP, focussing on calculations involving cohomology. We will describe the mathematics underlying the algorithms, and how to use them within GAP. Alexander Hulpke's lectures will being with some general computation
From playlist École d'Été 2022 - Cohomology Geometry and Explicit Number Theory
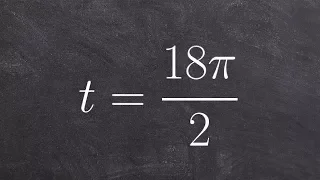
Find the coordinate point of the given angle
👉 Learn how to find the point on the unit circle given the angle of the point. A unit circle is a circle whose radius is 1. Given an angle in radians, to find the coordinate of points on the unit circle made by the given angle with the x-axis at the center of the unit circle, we plot the a
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)
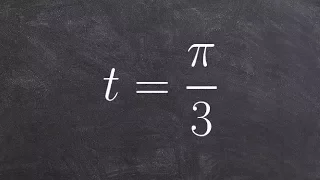
Find the coordinate point of the given angle
👉 Learn how to find the point on the unit circle given the angle of the point. A unit circle is a circle whose radius is 1. Given an angle in radians, to find the coordinate of points on the unit circle made by the given angle with the x-axis at the center of the unit circle, we plot the a
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)

Find the coordinate point of the given angle
👉 Learn how to find the point on the unit circle given the angle of the point. A unit circle is a circle whose radius is 1. Given an angle in radians, to find the coordinate of points on the unit circle made by the given angle with the x-axis at the center of the unit circle, we plot the a
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)

Find the coordinate point of the given angle
👉 Learn how to find the point on the unit circle given the angle of the point. A unit circle is a circle whose radius is 1. Given an angle in radians, to find the coordinate of points on the unit circle made by the given angle with the x-axis at the center of the unit circle, we plot the a
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)
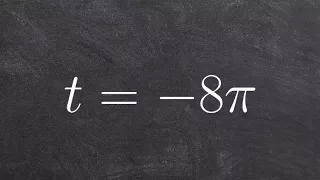
Find the coordinate point of the given angle
👉 Learn how to find the point on the unit circle given the angle of the point. A unit circle is a circle whose radius is 1. Given an angle in radians, to find the coordinate of points on the unit circle made by the given angle with the x-axis at the center of the unit circle, we plot the a
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)
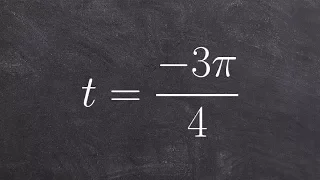
Find the coordinate point of the given angle
👉 Learn how to find the point on the unit circle given the angle of the point. A unit circle is a circle whose radius is 1. Given an angle in radians, to find the coordinate of points on the unit circle made by the given angle with the x-axis at the center of the unit circle, we plot the a
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)
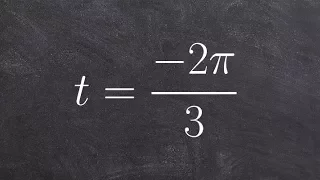
Find the coordinate point of the given angle
👉 Learn how to find the point on the unit circle given the angle of the point. A unit circle is a circle whose radius is 1. Given an angle in radians, to find the coordinate of points on the unit circle made by the given angle with the x-axis at the center of the unit circle, we plot the a
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)
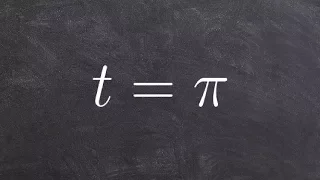
Find the coordinate point of the given angle
👉 Learn how to find the point on the unit circle given the angle of the point. A unit circle is a circle whose radius is 1. Given an angle in radians, to find the coordinate of points on the unit circle made by the given angle with the x-axis at the center of the unit circle, we plot the a
From playlist Evaluate Trigonometric Functions With The Unit Circle (ALG2)