
The Remainder Theorem - Example 2
Thanks to all of you who support me on Patreon. You da real mvps! $1 per month helps!! :) https://www.patreon.com/patrickjmt !! The Remainder Theorem - Example 2
From playlist Polynomials: Introduction

👉 Learn how to multiply fractions. To multiply fractions, we need to multiply the numerator by the numerator and multiply the denominator by the denominator. We then reduce the fraction. By reducing the fraction we are writing it in most simplest form. It is very important to understand t
From playlist How to Multiply Fractions

👉 Learn how to multiply fractions. To multiply fractions, we need to multiply the numerator by the numerator and multiply the denominator by the denominator. We then reduce the fraction. By reducing the fraction we are writing it in most simplest form. It is very important to understand t
From playlist How to Multiply Fractions

What is the remainder theorem for polynomials
👉 Learn about the remainder theorem and the factor theorem. The remainder theorem states that when a polynomial is divided by a linear expression of the form (x - k), the remainder from the division is equivalent to f(k). Similarly, when a polynomial is divided by a linear expression of th
From playlist Remainder and Factor Theorem | Learn About

Greatest Common Factor Trick GCF
It is easy to find the greatest common factor using the eucliean method. This is the fastest method of working out greatst common factors short of knowing all the factors for every number! This method works rapidly even for large numbers and utilises the Euclidean algorithm. To donate
From playlist Factors and Multilples
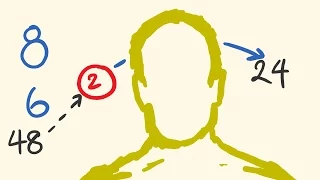
Least Common Multiple Trick LCM
This method for working Least Common Multiple is both rapid and 100% accurate, even for the most difficult examples. To support free math on Patreon (thank you): https://www.patreon.com/tecmath To donate to the tecmath channel: https://paypal.me/tecmath?locale.x=en_AU To donate to the tec
From playlist Factors and Multilples

Theory of numbers: Euclid's algorithm
This lecture is part of an online undergraduate course on the theory of numbers. We describe several algorithms for finding the greatest common divisor of two numbers. For the other lectures in the course see https://www.youtube.com/playlist?list=PL8yHsr3EFj52Qf7lc3HHvHRdIysxEcj1H
From playlist Theory of numbers

Algebra - Ch. 10: Rational Expression (24 of 33) What is the Remainder Theorem?
Visit http:ilectureonline.com for more math and science lectures! In this video I will explain by example of what is the Remainder Theorem. To donate: http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3236071 Next video in this series can be seen at: https://youtu.be/
From playlist ALGEBRA CH 10 RATIONAL EXPRESSIONS

Taylor's Remainder Theorem - Finding the Remainder, Ex 2
Thanks to all of you who support me on Patreon. You da real mvps! $1 per month helps!! :) https://www.patreon.com/patrickjmt !! Taylor's Remainder Theorem - Finding the Remainder, Ex 2. In this example, I use Taylor's Remainder Theorem to find an expression for the remainder.
From playlist Sequence and Series Video Tutorial

Checksum is a method of checking for errors in a communications system. I'm Mr. Woo and my channel is all about learning - I love doing it, and I love helping others to do it too. I guess that's why I became a teacher! I hope you get something out of these videos - I upload almost every w
From playlist Communications & Network Systems

From playlist CS50 Walkthroughs (Problem Sets)

Easy Rust 057: Collection types (BinaryHeap)
The rarely mentioned BinaryHeap can be pretty useful sometimes. From this chapter: https://dhghomon.github.io/easy_rust/Chapter_32.html #rustlang Want to buy me a coffee? Do it here: https://www.buymeacoffee.com/mithridates
From playlist Easy Rust / Rust in a Month of Lunches: bite-sized Rust tutorials

What is the Continuous Division Method for finding the HCF? | Don't Memorise
To access all videos related to HCF and LCM, enroll in our full course now: https://infinitylearn.com/microcourses?utm_source=youtube&utm_medium=Soical&utm_campaign=DM&utm_content=fAXlbjY1T_Q&utm_term=%7Bkeyword%7D In this video, we will learn: 0:00 The Continuous Division Method for fin
From playlist Middle School Arithmetic(Part 1)

Greatest Binomial Coefficient (5 of 5: Locating & evaluating the coefficient)
More resources available at www.misterwootube.com
From playlist Working with Combinatorics

Number Theory: Part 2: Chinese Remainder Theorem
Chinese Remainder Theorem is presented. Discrete Logarithms are analyzed.
From playlist Network Security

János Pintz: Large values of the remainder term of the prime number theorem
CIRM VIRTUAL CONFERENCE Recorded during the meeting " Diophantine Problems, Determinism and Randomness" the November 26, 2020 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide
From playlist Virtual Conference

Solving Cubic Equations - Benedict Gross
Speaker : Benedict Gross Date and Time : 06 Jan 12, 17:15 Venue : AG 66, TIFR, Mumbai I will discuss a problem which has been central in number theory for several centuries -- whether a cubic equation in the plane has infinitely many rational solutions.This led to a precise conjecture by
From playlist Public Lectures
Remainder & Factor Theorem (1 of 2: How do we calculate remainders without dividing?)
More resources available at www.misterwootube.com
From playlist Further Polynomials

Bairstow's Method for finding the roots of polynomials including complex roots. Discussion of method derivation, relation to synthetic division of two variables, stopping condition, selection of initial values, fractals, and historical context. Submission for Summer of Math Exposition 2 co
From playlist Root Finding
