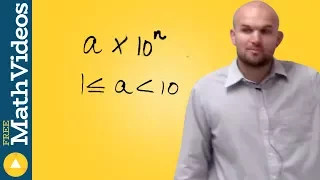
What is the definition of scientific notation
👉 Learn about scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is the number of digits up to t
From playlist Scientific Notation | Learn About

Dividing two numbers in scientific notation
👉 Learn how to divide numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is t
From playlist Scientific Notation
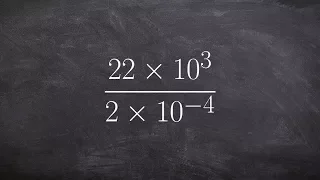
Dividing two numbers in scientific notation then rewriting answer in scientific notation
👉 Learn how to divide numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is t
From playlist Scientific Notation

Finding the quotient for two numbers while in scientific notation
👉 Learn how to divide numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is t
From playlist Scientific Notation
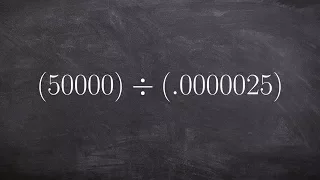
Find the quotient between two numbers by converting to scientific notation
👉 Learn how to divide numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is t
From playlist Scientific Notation

Learn how to divide two numbers in scientific notation
👉 Learn how to divide numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is t
From playlist Scientific Notation
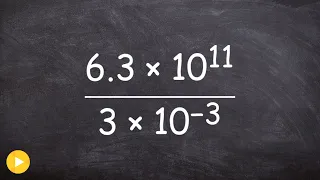
Learn how to divide two numbers in scientific notation
👉 Learn how to divide numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is t
From playlist Scientific Notation
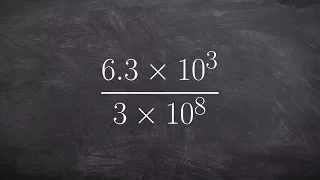
Determining the quotient of two numbers in scientific notation
👉 Learn how to divide numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is t
From playlist Scientific Notation

Backpropagation explained | Part 2 - The mathematical notation
We covered the intuition behind what backpropagation's role is during the training of an artificial neural network. https://youtu.be/XE3krf3CQls Now, we're going to focus on the math that's underlying backprop. The math is pretty involved, and so we're going to break it up into bite-size
From playlist Deep Learning Fundamentals - Intro to Neural Networks

Determine the product of two very large numbers by converting to scientific notation
👉 Learn how to multiply numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is
From playlist Scientific Notation

L4.2 The uncoupled and coupled basis states for the spectrum
MIT 8.06 Quantum Physics III, Spring 2018 Instructor: Barton Zwiebach View the complete course: https://ocw.mit.edu/8-06S18 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP60Zcz8LnCDFI8RPqRhJbb4L L4.2 The uncoupled and coupled basis states for the spectrum License: Cre
From playlist MIT 8.06 Quantum Physics III, Spring 2018
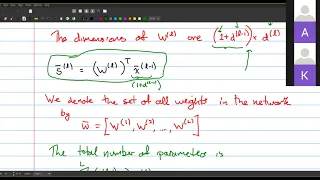
Neural Networks: Forward and Back propagation
From playlist MachineLearning

Tides in binary star systems (Lecture - 01) by Tanja Hinderer
Summer School on Gravitational-Wave Astronomy DATE: 17 July 2017 to 28 July 2017 VENUE: Madhava Lecture Hall, ICTS Bangalore This school is a part of the annual ICTS summer schools in gravitational wave astronomy. This year’s school will focus on the physics and astrophysics of compact
From playlist Summer School on Gravitational-Wave Astronomy - 2017

But what *is* a Neural Network? - THE MATH YOU SHOULD KNOW!
We'll take a look at how exactly neural networks learn by starting with modeling an objective function through Maximum Likelihood Estimation. We then take a look at neural network training using back propagation and Stochastic gradient descent. FOLLOW ME https://www.quora.com/profile/Ajay
From playlist The Math You Should Know

Noncommutative Geometric Invariant Theory (Lecture 2) by Arvid Siqveland
PROGRAM :SCHOOL ON CLUSTER ALGEBRAS ORGANIZERS :Ashish Gupta and Ashish K Srivastava DATE :08 December 2018 to 22 December 2018 VENUE :Madhava Lecture Hall, ICTS Bangalore In 2000, S. Fomin and A. Zelevinsky introduced Cluster Algebras as abstractions of a combinatoro-algebra
From playlist School on Cluster Algebras 2018

MIT 3.60 | Lec 24a: Symmetry, Structure, Tensor Properties of Materials
Part 1: Piezoelectricity (cont.) View the complete course at: http://ocw.mit.edu/3-60F05 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 3.60 Symmetry, Structure & Tensor Properties of Material

Lecture 20 | The Fourier Transforms and its Applications
Lecture by Professor Brad Osgood for the Electrical Engineering course, The Fourier Transforms and its Applications (EE 261). Professor Osgood continues his lecture on the Discrete Fourier Transform. The Fourier transform is a tool for solving physical problems. In this course the emph
From playlist Lecture Collection | The Fourier Transforms and Its Applications

Recent Advances on Beilinson-Bloch-Kato Conjecture (Lecture 2) by Yifeng Liu
PROGRAM ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (HYBRID) ORGANIZERS: Ashay Burungale (CalTech/UT Austin, USA), Haruzo Hida (UCLA), Somnath Jha (IIT Kanpur) and Ye Tian (MCM, CAS) DATE: 08 August 2022 to 19 August 2022 VENUE: Ramanujan Lecture Hall and online The program pla
From playlist ELLIPTIC CURVES AND THE SPECIAL VALUES OF L-FUNCTIONS (2022)

Raising a scientific number to the third power
👉 Learn how to multiply numbers written in scientific notations. Scientific notation is a convenient way of writing very large or very small numbers. A number written in scientific notation is of the form a * 10^n where a is the first non-zero number between 1 and 10, (1 included) and n is
From playlist Scientific Notation
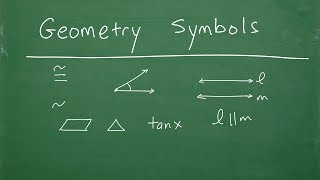
GEOMETRY Basics – Introduction to Common Notations and Symbols
https://tabletclass-academy.teachable.com/p/tabletclass-math-geometry1 TabletClass Math: https://tcmathacademy.com/ This video goes over geometry notation and symbols.
From playlist Geometry