
Norbert Mauser: The quantum Vlasov equation
Abstract: We present the Quantum Vlasov or Wigner equation as a "phase space" presentation of quantum mechanics that is close to the classical Vlasov equation, but where the "distribution function" w(x,v,t) will in general have also negative values. We discuss the relation to the classical
From playlist Mathematical Physics

Amir Ali Ahmadi, Princeton University
January 31, Amir Ali Ahmadi, Princeton University Two Problems at the Interface of Optimization and Dynamical Systems We propose and/or analyze semidefinite programming-based algorithms for two problems at the interface of optimization and dynamical systems: In part (i), we study the po
From playlist Spring 2020 Kolchin Seminar in Differential Algebra

Dimitri Zvonkine - On two ELSV formulas
The ELSV formula (discovered by Ekedahl, Lando, Shapiro and Vainshtein) is an equality between two numbers. The first one is a Hurwitz number that can be defined as the number of factorizations of a given permutation into transpositions. The second is the integral of a characteristic class
From playlist 4th Itzykson Colloquium - Moduli Spaces and Quantum Curves
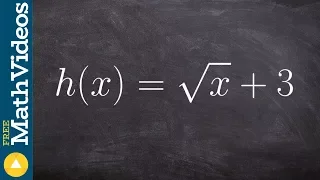
How to determine if an equation is a linear relation
👉 Learn how to determine if an equation is a linear equation. A linear equation is an equation whose highest exponent on its variable(s) is 1. The variables do not have negative or fractional, or exponents other than one. Variables must not be in the denominator of any rational term and c
From playlist Write Linear Equations

C07 Homogeneous linear differential equations with constant coefficients
An explanation of the method that will be used to solve for higher-order, linear, homogeneous ODE's with constant coefficients. Using the auxiliary equation and its roots.
From playlist Differential Equations

Maxim Kazarian - 1/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

Maxim Kazarian - 2/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

Andreï Kolmogorov: un grand mathématicien au coeur d'un siècle tourmenté
Conférence grand public au CIRM Luminy Andreï Kolmogorov est un mathématicien russe (1903-1987) qui a apporté des contributions frappantes en théorie des probabilités, théorie ergodique, turbulence, mécanique classique, logique mathématique, topologie, théorie algorithmique de l'informati
From playlist OUTREACH - GRAND PUBLIC

The Large-Scale Dynamics of Flows: Facts and Proofs from 1D Burgers to 3D Euler/NS by Uriel Frisch
Program Turbulence: Problems at the Interface of Mathematics and Physics (ONLINE) ORGANIZERS: Uriel Frisch (Observatoire de la Côte d'Azur and CNRS, France), Konstantin Khanin (University of Toronto, Canada) and Rahul Pandit (Indian Institute of Science, Bengaluru) DATE: 07 December 202
From playlist Turbulence: Problems at The Interface of Mathematics and Physics (Online)

Nicola Garofalo: Hypoelliptic operators and analysis on Carnot-Carathéodory spaces
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Algebraic and Complex Geometry

Method of Undetermined Coefficients
We demonstrate how to solve 2nd order, linear, inhomogeneous differential equations with the Method of Undetermined Coefficients.
From playlist Mathematical Physics I Uploads

Maxim Kazarian - 3/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

Clément Mouhot: Quantitative De Giorgi methods in kinetic theory
CIRM VIRTUAL EVENT Recorded during the meeting "Kinetic Equations: from Modeling, Computation to Analysis" the March 23, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide m
From playlist Virtual Conference

Nexus Trimester - Andrei Romashchenko (LIRMM)
On Parallels Between Shannon’s and Kolmogorov’s Information Theories (where the parallelism fails and why) Andrei Romashchenko (LIRMM) February 02, 2016 Abstract: Two versions of information theory - the theory of Shannon's entropy and the theory of Kolmgorov complexity - have manifest
From playlist Nexus Trimester - 2016 - Distributed Computation and Communication Theme

Statistical Properties of the Navier-Stokes-Voigt Model by Edriss S. Titi
Program Turbulence: Problems at the Interface of Mathematics and Physics (ONLINE) ORGANIZERS: Uriel Frisch (Observatoire de la Côte d'Azur and CNRS, France), Konstantin Khanin (University of Toronto, Canada) and Rahul Pandit (Indian Institute of Science, Bengaluru) DATE: 07 December 202
From playlist Turbulence: Problems at The Interface of Mathematics and Physics (Online)

Turbulence Energy Spectrum by Jayanta K. Bhattacharjee
Program Turbulence: Problems at the Interface of Mathematics and Physics (ONLINE) ORGANIZERS: Uriel Frisch (Observatoire de la Côte d'Azur and CNRS, France), Konstantin Khanin (University of Toronto, Canada) and Rahul Pandit (Indian Institute of Science, Bengaluru) DATE: 07 December 202
From playlist Turbulence: Problems at The Interface of Mathematics and Physics (Online)

Order, disorder and entropy (Lecture - 01) by Daan Frenkel
INFOSYS-ICTS CHANDRASEKHAR LECTURES FROM SELF-ASSEMBLY TO CELL RECOGNITION Daan Frenkel (University of Cambridge, UK) DATE :29 August 2018, 16:00 to 17:00 VENUE:Ramanujan Lecture Hall, ICTS Bangalore. Lecture 1: Tuesday 28 August, 16:00 to 17:00 Title : Order, disorder and entropy Ab
From playlist Infosys-ICTS Chandrasekhar Lectures

The fascinating world of turbulent flows by Samriddhi Sankar Ray
EINSTEIN LECTURES THE FASCINATING WORLD OF TURBULENT FLOWS SPEAKER: Samriddhi Sankar Ray (International Centre for Theoretical Sciences) DATE: 24 August 2018, 12:00 VENUE: Dayananda Sagar College of Engineering, Kumarswamy Layout, Bengaluru - 78 Turbulent flows are ubiquitous. They ar
From playlist Einstein Lectures
Introduction to Parametric Equations
This video defines a parametric equations and shows how to graph a parametric equation by hand. http://mathispower4u.yolasite.com/
From playlist Parametric Equations

Status of experiments and simulations on scaling problems in turbulence - Katepalli Sreenivasan
Workshop on Turbulence Topic: Status of experiments and simulations on scaling problems in turbulence Speaker: Katepalli Sreenivasan Affiliation: New York University Date: December 11, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics