
Introduction to additive combinatorics lecture 10.8 --- A weak form of Freiman's theorem
In this short video I explain how the proof of Freiman's theorem for subsets of Z differs from the proof given earlier for subsets of F_p^N. The answer is not very much: the main differences are due to the fact that cyclic groups of prime order do not have lots of subgroups, so one has to
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Greg Kleiman on Red Hat's expansion into data - Strata Europe 2014
From Strata + Hadoop World Europe 2014 in Barcelona, an interview with the Director of Red Hat about their move into the data world and what sets them apart from data-oriented companies. Watch more from Strata Europe 2014: http://goo.gl/uqw6WS Visit the Strata website to learn more: http:
From playlist Strata + Hadoop World in Europe 2014

Steven Kleiman - "Equisingularity of germs of isolated singularities"
Steven Kleiman delivers a research lecture at the Worldwide Center of Mathematics.
From playlist Center of Math Research: the Worldwide Lecture Seminar Series

Maxim Kazarian - 1/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

Using Shark Skin to Fight Against Bacteria | Think Like a Tree
Scientists are looking to an unlikely source for new ways to fight bacteria. Could the skin of a Galapagos shark hold the key to warding off hospital-born bacteria and superbugs? SUBSCRIBE for more videos: http://wrd.cm/15fP7B7 Still haven’t subscribed to WIRED on YouTube? ►► http://wr
From playlist It's World Ocean Week! Let's Learn About Ocean Animals!

Computer History: 1946 ENIAC Computer History Remastered FULL VERSION First Electronic Computer U.S.
Computer History: ENIAC Computer History, an educational film: The First Large Scale, Programmable, General Purpose Electronic Digital Computer ~ ENIAC - original 1946 announcement film, restored & new narration. ENIAC, "Electronic Numerical Integrator and Computer", was designed by J.
From playlist Computer History: ENIAC 1944-1946: Origin and History of a Giant Brain

Maxim Kazarian - 2/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

P. Scholze - p-adic K-theory of p-adic rings
The original proof of Grothendieck's purity conjecture in étale cohomology (the Thomason-Gabber theorem) relies on results on l-adic K-theory and its relation to étale cohomology when l is invertible. Using recent advances of Clausen-Mathew-Morrow and joint work with Bhatt and Morrow, our
From playlist Arithmetic and Algebraic Geometry: A conference in honor of Ofer Gabber on the occasion of his 60th birthday

Positive cones of higher (co)dimensional numerical cycle classes - Mihai Fulger
Mihai Fulger Princeton University October 21, 2014 It is classical to study the geometry of projective varieties over algebraically closed fields through the properties of various positive cones of divisors or curves. Several counterexamples have shifted attention from the higher (co)dime
From playlist Mathematics

Math 131 Fall 2018 100318 Heine Borel Theorem
Definition of limit point compactness. Compact implies limit point compact. A nested sequence of closed intervals has a nonempty intersection. k-cells are compact. Heine-Borel Theorem: in Euclidean space, compactness, limit point compactness, and being closed and bounded are equivalent
From playlist Course 7: (Rudin's) Principles of Mathematical Analysis (Fall 2018)

R. Lazarsfeld: The Equations Defining Projective Varieties. Part 1
The lecture was held within the framework of the Junior Hausdorff Trimester Program Algebraic Geometry. (7.1.2014)
From playlist HIM Lectures: Junior Trimester Program "Algebraic Geometry"

Aaron Silberstein - Plane Curve Singularities and the Absolute Galois Group of Q
Plane Curve Singularities and the Absolute Galois Group of Q
From playlist Center of Math Research: the Worldwide Lecture Seminar Series

Max Kleiman-Weiner - Multi-Agent Common Sense - IPAM at UCLA
Recorded 16 February 2022. Max Kleiman-Weiner of Common Sense Machines presents "Multi-Agent Common Sense" at IPAM's Mathematics of Collective Intelligence Workshop. Abstract: Human collective intelligence is distinctly powerful. We collaborate with others to accomplish together what none
From playlist Workshop: Mathematics of Collective Intelligence - Feb. 15 - 19, 2022.
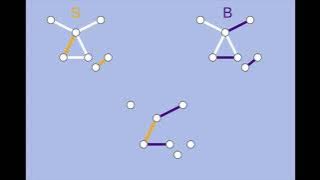
Berge's lemma, an animated proof
Berge's lemma is a mathematical theorem in graph theory which states that a matching in a graph is of maximum cardinality if and only if it has no augmenting paths. But what do those terms even mean? And how do we prove Berge's lemma to be true? == CORRECTION: at 7:50, the red text should
From playlist Summer of Math Exposition Youtube Videos

Maxim Kazarian - 3/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

Introduction to additive combinatorics lecture 1.8 --- Plünnecke's theorem
In this video I present a proof of Plünnecke's theorem due to George Petridis, which also uses some arguments of Imre Ruzsa. Plünnecke's theorem is a very useful tool in additive combinatorics, which implies that if A is a set of integers such that |A+A| is at most C|A|, then for any pair
From playlist Introduction to Additive Combinatorics (Cambridge Part III course)

Parahoric Torsors and Degeneration of Moduli Spaces by Vikraman Balaji
Program Quantum Fields, Geometry and Representation Theory 2021 (ONLINE) ORGANIZERS: Aswin Balasubramanian (Rutgers University, USA), Indranil Biswas (TIFR, india), Jacques Distler (The University of Texas at Austin, USA), Chris Elliott (University of Massachusetts, USA) and Pranav Pandi
From playlist Quantum Fields, Geometry and Representation Theory 2021 (ONLINE)

Proof of Lemma and Lagrange's Theorem
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proof of Lemma and Lagrange's Theorem. This video starts by proving that any two right cosets have the same cardinality. Then we prove Lagrange's Theorem which says that if H is a subgroup of a finite group G then the order of H div
From playlist Abstract Algebra

The Campbell-Baker-Hausdorff and Dynkin formula and its finite nature
In this video explain, implement and numerically validate all the nice formulas popping up from math behind the theorem of Campbell, Baker, Hausdorff and Dynkin, usually a.k.a. Baker-Campbell-Hausdorff formula. Here's the TeX and python code: https://gist.github.com/Nikolaj-K/8e9a345e4c932
From playlist Algebra

Hilbert's 15th Problem: Schubert Calculus | Infinite Series
Viewers like you help make PBS (Thank you 😃) . Support your local PBS Member Station here: https://to.pbs.org/donateinfi Get 2 months of Curiosity Stream free by going to www.curiositystream.com/infinite and signing up with the promo code "infinite." It's said that Hermann Schubert perfor
From playlist An Infinite Playlist