
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations

What is an enlargement dilation
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations
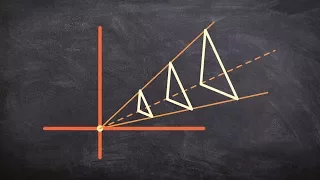
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations

Overview transformations horizontal shifts - Online Tutor - Free Math Videos
👉 Learn how to determine the transformation of a function. Transformations can be horizontal or vertical, cause stretching or shrinking or be a reflection about an axis. You will see how to look at an equation or graph and determine the transformation. You will also learn how to graph a t
From playlist Characteristics of Functions
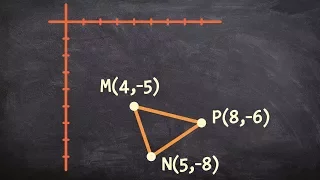
Shifting a triangle using a transformation vector
👉 Learn how to apply transformations of a figure and on a plane. We will do this by sliding the figure based on the transformation vector or directions of translations. When performing a translation we are sliding a given figure up, down, left or right. The orientation and size of the fi
From playlist Transformations
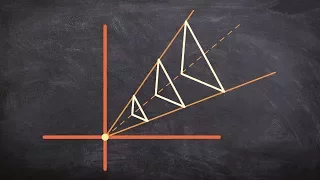
What are dilations, similarity and scale factors
👉 Learn about dilations. Dilation is the transformation of a shape by a scale factor to produce an image that is similar to the original shape but is different in size from the original shape. A dilation that creates a larger image is called an enlargement or a stretch while a dilation tha
From playlist Transformations

An intro to basic transformations of functions. Covers the transformations -y=f(x) and y=f(-x)
From playlist everything

Four types of transformations and introduction of transformation | Geometry Transformations in 3D
In this video you have learn four types of transformations and introduction of transformation. 4 types of transformations are Reflection Rotation Symmetry Shift #mathstransformations, #maths, #Grade 9 maths,
From playlist Maths Topics

Transformations of a function - How to do Pre-Calc
👉 Learn how to determine the transformation of a function. Transformations can be horizontal or vertical, cause stretching or shrinking or be a reflection about an axis. You will see how to look at an equation or graph and determine the transformation. You will also learn how to graph a t
From playlist Characteristics of Functions

Compositional Structure of Classical Integral Transforms
The recently implemented fractional order integro-differentiation operator, FractionalD, is a particular case of more general integral transforms. The majority of classical integral transforms are representable as compositions of only two transforms: the modified direct and inverse Laplace
From playlist Wolfram Technology Conference 2022

Lecture 22, The z-Transform | MIT RES.6.007 Signals and Systems, Spring 2011
Lecture 22, The z-Transform Instructor: Alan V. Oppenheim View the complete course: http://ocw.mit.edu/RES-6.007S11 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT RES.6.007 Signals and Systems, 1987

Lecture 7 | The Fourier Transforms and its Applications
Lecture by Professor Brad Osgood for the Electrical Engineering course, The Fourier Transforms and its Applications (EE 261). Professor Osgood reintroduces the Fourier Transform and its inverse, then he goes into specific properties and transforms. The Fourier transform is a tool for s
From playlist Lecture Collection | The Fourier Transforms and Its Applications

Lecture 13 | The Fourier Transforms and its Applications
Lecture by Professor Brad Osgood for the Electrical Engineering course, The Fourier Transforms and its Applications (EE 261). In this lecture, Professor Osgood demonstrates Fourier transforms of a general distribution. The Fourier transform is a tool for solving physical problems. In t
From playlist Lecture Collection | The Fourier Transforms and Its Applications

ME565 Lecture 21: The Laplace Transform
ME565 Lecture 21 Engineering Mathematics at the University of Washington Laplace Transform Notes: http://faculty.washington.edu/sbrunton/me565/pdf/L21.pdf Course Website: http://faculty.washington.edu/sbrunton/me565/ http://faculty.washington.edu/sbrunton/
From playlist Engineering Mathematics (UW ME564 and ME565)

Lec 5 | MIT RES.6-008 Digital Signal Processing, 1975
Lecture 5: The z-transform Instructor: Alan V. Oppenheim View the complete course: http://ocw.mit.edu/RES6-008S11 License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT RES.6-008 Digital Signal Processing, 1975

The Laplace Transform: A Generalized Fourier Transform
This video is about the Laplace Transform, a powerful generalization of the Fourier transform. It is one of the most important transformations in all of science and engineering. @eigensteve on Twitter Brunton Website: eigensteve.com Book Website: http://databookuw.com Book PDF: http:/
From playlist Data-Driven Science and Engineering
Lecture: The Z transform 2018-10-29
This (long) video takes you all the way through the process of understanding the Z transform and how it relates to the Laplace transform for simulation.
From playlist Discrete

Laplace Transform: First Order Equation
MIT RES.18-009 Learn Differential Equations: Up Close with Gilbert Strang and Cleve Moler, Fall 2015 View the complete course: http://ocw.mit.edu/RES-18-009F15 Instructor: Gilbert Strang Transform each term in the linear differential equation to create an algebra problem. You can transfor
From playlist Fourier

Overview transformations, vertical shifts - Online Tutor - Free Math Videos
👉 Learn how to determine the transformation of a function. Transformations can be horizontal or vertical, cause stretching or shrinking or be a reflection about an axis. You will see how to look at an equation or graph and determine the transformation. You will also learn how to graph a t
From playlist Characteristics of Functions

Lecture with Ole Christensen. Kapitler: 00:00 - Reaching The Goal; 05:00 - Problem With The Fourier Transform; 13:45 - Where Does The Fourier Transform Map Into?; 16:45 - Is F Bounded?; 20:00 - Fourier Transform On L2; 30:00 - Using The Extension Theorem;
From playlist DTU: Mathematics 4 Real Analysis | CosmoLearning.org Math