
Monotonicity of the Riemann zeta function and related functions - P Zvengrowski [2012]
General Mathematics Seminar of the St. Petersburg Division of Steklov Institute of Mathematics, Russian Academy of Sciences May 17, 2012 14:00, St. Petersburg, POMI, room 311 (27 Fontanka) Monotonicity of the Riemann zeta function and related functions P. Zvengrowski University o
From playlist Number Theory

Dimitri Grigoryev - A Tropical Version of Hilbert Polynomial
We define Hilbert function of a semiring ideal of tropical polynomials in n variables. For n=1 we prove that it is the sum of a linear function and a periodic function (for sufficiently large values). The leading coefficient of the linear function equals the tropical entropy of the ideal.
From playlist Combinatorics and Arithmetic for Physics: special days

Z. Badreddine - Optimal transportation problem and MCP property on sub-Riemannian structures
This presentation is devoted to the study of mass transportation on sub-Riemannian geometry. In order to obtain existence and uniqueness of optimal transport maps, the first relevant method to consider is the one used by Figalli and Rifford which is based on the local semiconcavity of the
From playlist Journées Sous-Riemanniennes 2018

Prob & Stats - Bayes Theorem (1 of 24) What is Bayes Theorem?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what is and define the symbols of Bayes Theorem. Bayes Theorem calculates the probability of an event or the predictive value of an outcome of a test based on prior knowledge of condition rela
From playlist PROB & STATS 4 BAYES THEOREM

Maxim Kazarian - 1/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

Decision Making and Inference Under Model Misspecification by Jose Blanchet
PROGRAM: ADVANCES IN APPLIED PROBABILITY ORGANIZERS: Vivek Borkar, Sandeep Juneja, Kavita Ramanan, Devavrat Shah, and Piyush Srivastava DATE & TIME: 05 August 2019 to 17 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Applied probability has seen a revolutionary growth in resear
From playlist Advances in Applied Probability 2019

Robert MacCann - Optimal Transport - Lecture 1
1. Introduction 2. References 1:43 Guillen and MacCann: http://www.math.toronto.edu/mccann/papers/FiveLectures.pdf MacCann: http://www.math.toronto.edu/mccann/papers/glimpse.pdf Chiappori, MacCann and Pass: http://www.math.toronto.edu/mccann/papers/CMPMath.pdf Chiappori, MacCann and Pass:
From playlist 2016 - Calculus of Variations and PDE's

Optimal Transport (According to Leonid Kantorovich)
Kantorovich problem of Optimal Transport, definition and some context. See for example Villani - Topics in Optimal Transport (2003), Chapter 1 or Ambosio Gigli - A users guide to Optimal Transport (2008), Chapter 1.1.
From playlist Optimal Transport

What is the Riemann Hypothesis?
This video provides a basic introduction to the Riemann Hypothesis based on the the superb book 'Prime Obsession' by John Derbyshire. Along the way I look at convergent and divergent series, Euler's famous solution to the Basel problem, and the Riemann-Zeta function. Analytic continuation
From playlist Mathematics

Maxim Kazarian - 2/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

Benedetto Piccoli: "Social dynamics, control of large groups and vehicular traffic"
Mathematical Challenges and Opportunities for Autonomous Vehicles 2020 Workshop IV: Social Dynamics beyond Vehicle Autonomy "Social dynamics, control of large groups and vehicular traffic" Benedetto Piccoli - Rutgers University Abstract: We revise come recent approach to model social dyn
From playlist Mathematical Challenges and Opportunities for Autonomous Vehicles 2020

Concentration of quantum states from quantum functional (...) - N. Datta - Workshop 2 - CEB T3 2017
Nilanjana Datta / 24.10.17 Concentration of quantum states from quantum functional and transportation cost inequalities Quantum functional inequalities (e.g. the logarithmic Sobolev- and Poincaré inequalities) have found widespread application in the study of the behavior of primitive q
From playlist 2017 - T3 - Analysis in Quantum Information Theory - CEB Trimester

Matthias Liero: On entropy transport problems and the Hellinger Kantorovich distance
In this talk, we will present a general class of variational problems involving entropy-transport minimization with respect to a couple of given finite measures with possibly unequal total mass. These optimal entropy-transport problems can be regarded as a natural generalization of classic
From playlist HIM Lectures: Follow-up Workshop to JTP "Optimal Transportation"

From playlist Contributed talks One World Symposium 2020

Maxim Kazarian - 3/3 Mathematical Physics of Hurwitz numbers
Hurwitz numbers enumerate ramified coverings of a sphere. Equivalently, they can be expressed in terms of combinatorics of the symmetric group; they enumerate factorizations of permutations as products of transpositions. It turns out that these numbers obey a huge num
From playlist Physique mathématique des nombres de Hurwitz pour débutants

The Field With One Element and The Riemann Hypothesis (Full Video)
A crash course of Deninger's program to prove the Riemann Hypothesis using a cohomological interpretation of the Riemann Zeta Function. You can Deninger talk about this in more detail here: http://swc.math.arizona.edu/dls/ Leave some comments!
From playlist Riemann Hypothesis

Optimal Transport Methods and Applications to Statistics and... (Lecture 2) by Jose Blanchet
PROGRAM: ADVANCES IN APPLIED PROBABILITY ORGANIZERS: Vivek Borkar, Sandeep Juneja, Kavita Ramanan, Devavrat Shah, and Piyush Srivastava DATE & TIME: 05 August 2019 to 17 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Applied probability has seen a revolutionary growth in resear
From playlist Advances in Applied Probability 2019
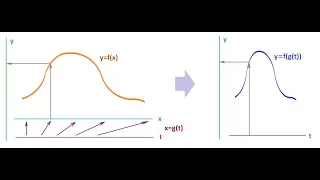
Change of variables and the derivative -- Calculus I
This lecture is on Calculus I. It follows Part I of the book Calculus Illustrated by Peter Saveliev. The text of the book can be found at http://calculus123.com.
From playlist Calculus I

We define the Kantorovich dual of Kantorovich problem of Optimal Transport and give a (well known) interpretation in terms of "outsourcing" the task of transporting goods.
From playlist Optimal Transport
