
What is the alternate in sign sequence
👉 Learn about sequences. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. There are many types of sequence, among which are: arithmetic and geometric sequence. An arithmetic sequence is a sequence in which
From playlist Sequences

What is an arithmetic sequence
👉 Learn about sequences. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. There are many types of sequence, among which are: arithmetic and geometric sequence. An arithmetic sequence is a sequence in which
From playlist Sequences

What is the formula for the rule for the nth term of a arithmetic sequence
👉 Learn about sequences. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. There are many types of sequence, among which are: arithmetic and geometric sequence. An arithmetic sequence is a sequence in which
From playlist Sequences

Introduction to Sequences (Discrete Math)
This video introduces sequences for a discrete math class. mathispower4u.com
From playlist Sequences (Discrete Math)
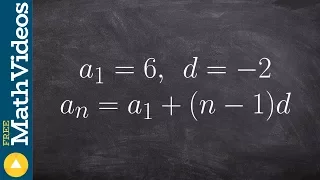
How to determine the rule of a arithmetic sequence given a1 and d
👉 Learn how to write the explicit formula for the nth term of an arithmetic sequence. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. An arithmetic sequence is a sequence in which each term of the sequence
From playlist Sequences

What is the difference between finite and infinite sequences
👉 Learn about sequences. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. There are many types of sequence, among which are: arithmetic and geometric sequence. An arithmetic sequence is a sequence in which
From playlist Sequences

Finding the rule of the sequence using multiplication and addition
👉 Learn how to write the explicit formula for the nth term of an arithmetic sequence. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. An arithmetic sequence is a sequence in which each term of the sequence
From playlist Sequences

How to find the rule of a arithmetic sequence given two values in the sequence
👉 Learn how to write the explicit formula for the nth term of an arithmetic sequence. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. An arithmetic sequence is a sequence in which each term of the sequence
From playlist Sequences

Daniel Smertnig, University of Graz
October 28, Daniel Smertnig, University of Graz A height gap theorem for coefficients of Mahler functions
From playlist Fall 2022 Online Kolchin seminar in Differential Algebra

👉 Learn about sequences. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. There are many types of sequence, among which are: arithmetic and geometric sequence. An arithmetic sequence is a sequence in which
From playlist Sequences

16. Graph limits III: compactness and applications
MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019 Instructor: Yufei Zhao View the complete course: https://ocw.mit.edu/18-217F19 YouTube Playlist: https://www.youtube.com/playlist?list=PLUl4u3cNGP62qauV_CpT1zKaGG_Vj5igX Continuing the discussion of graph limits, Prof. Zhao pro
From playlist MIT 18.217 Graph Theory and Additive Combinatorics, Fall 2019

Jason P. Bell: Applications of algebra to automatic sequences and pattern avoidance - Lecture 1
Abstract: We will cover some of the more important results from commutative and noncommutative algebra as far as applications to automatic sequences, pattern avoidance, and related areas. Well give an overview of some applications of these areas to the study of automatic and regular sequen
From playlist Mathematical Aspects of Computer Science

Leray spectral sequence continued, computing derived pushforwards, strict henselizations and stalks of derived pushforwards, Weil-Divisor exact sequence, cohomology of the sheaf of divisors, reduction to Galois cohomology, intro to Brauer groups
From playlist Étale cohomology and the Weil conjectures

Charles Weibel: K-theory of line bundles and smooth varieties
The lecture was held within the framework of the Hausdorff Trimester Program: K-Theory and Related Fields. We give a K-theoretic criterion for a quasi-projective variety to be smooth, generalizing the proof of Vorst's conjecture for affine varieties. If L is a line bundle corresponding to
From playlist HIM Lectures: Trimester Program "K-Theory and Related Fields"

Juhani Karhumäki : k-abelian equivalence: an equivalence relation in between the equality...
Recording during the thematic meeting: "Combinatorics on Words" the March 16, 2016 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathemati
From playlist Combinatorics

Weil conjectures 6: etale cohomology of a curve
We give an overview of how to calculate the etale cohomology of a nonsinguar projective curve over an algebraically closed field with coefficients Z/nZ with n invertible. We simply assume a lot of properties of etale cohomology without proving (or even defining) them.
From playlist Algebraic geometry: extra topics

Jarosław Buczyński (6/29/17) Bedlewo: Constructions of k-regular maps using finite local schemes
A continuous map R^m → R^N or C^m → C^N is called k-regular if the images of any k distinct points are linearly independent. Given integers m and k a problem going back to Chebyshev and Borsuk is to determine the minimal value of N for which such maps exist. The methods of algebraic topolo
From playlist Applied Topology in Będlewo 2017

Commutative algebra 66: Local complete intersection rings
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. We define local complete intersection rings as regular local rings divided by a regular sequence. We give a few examples to il
From playlist Commutative algebra

Learn how to determine the rule given the first five terms of a sequence
👉 Learn how to write the explicit formula for the nth term of an arithmetic sequence. A sequence is a list of numbers/values exhibiting a defined pattern. A number/value in a sequence is called a term of the sequence. An arithmetic sequence is a sequence in which each term of the sequence
From playlist Sequences
