Ising critical exponents

Critical exponents (phase transitions)

This article lists the critical exponents of the ferromagnetic transition in the Ising model. In statistical physics, the Ising model is the simplest system exhibiting a continuous phase transition with a scalar order parameter and symmetry. The critical exponents of the transition are universal values and characterize the singular properties of physical quantities. The ferromagnetic transition of the Ising model establishes an important universality class, which contains a variety of phase transitions as different as ferromagnetism close to the Curie point and critical opalescence of liquid near its critical point. From the quantum field theory point of view, the critical exponents can be expressed in terms of scaling dimensions of the local operators of the conformal field theory describing the phase transition (In the Ginzburg–Landau description, these are the operators normally called .) These expressions are given in the last column of the above table, and were used to calculate the values of the critical exponents using the operator dimensions values from the following table: In d=2, the two-dimensional critical Ising model's critical exponents can be computed exactly using the minimal model . In d=4, it is the free massless scalar theory (also referred to as mean field theory). These two theories are exactly solved, and the exact solutions give values reported in the table. The d=3 theory is not yet exactly solved. This theory has been traditionally studied by the renormalization group methods and Monte-Carlo simulations. The estimates following from those techniques, as well as references to the original works, can be found in Refs. and. More recently, a conformal field theory method known as the conformal bootstrap has been applied to the d=3 theory. This method gives results in agreement with the older techniques, but up to two orders of magnitude more precise. These are the values reported in the table. (Wikipedia).

How to determine the global max and min from a piecewise function

👉 Learn how to find the extreme values of a function using the extreme value theorem. The extreme values of a function are the points/intervals where the graph is decreasing, increasing, or has an inflection point. A theorem which guarantees the existence of the maximum and minimum points

From playlist Extreme Value Theorem of Functions

Definition of a Critical Number with Examples

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Definition of a Critical Number with Examples

From playlist Calculus 1 Exam 2 Playlist

Find the critical values of an absolute value function

👉 Learn how to find the critical values of a function. The critical values of a function are the points where the graph turns. They are also called the turning points of a function. To obtain the critical points of a function, first, we obtain the first derivative of the function. Next, w

From playlist Find the Critical Values of a Function

How to Find Critical Numbers

Definition of critical numbers and two examples of how to find critical numbers for a polynomial and a rational function.

From playlist Calculus

Ian McCulloch: "Finite-entanglement scaling functions at quantum critical points"

Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021 Workshop II: Tensor Network States and Applications "Finite-entanglement scaling functions at quantum critical points" Ian McCulloch - University of Queensland Abstract: For translationally invariant infinite

From playlist Tensor Methods and Emerging Applications to the Physical and Data Sciences 2021

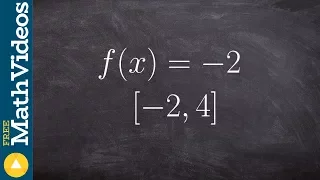
What is the max and min of a horizontal line on a closed interval

From playlist Extreme Value Theorem of Functions

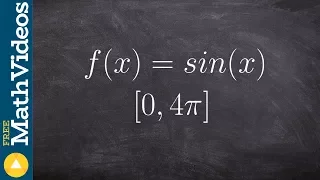
How to determine the max and min of a sine on a closed interval

From playlist Extreme Value Theorem of Functions

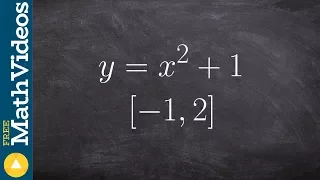
Find the max and min from a quadratic on a closed interval

From playlist Extreme Value Theorem of Functions

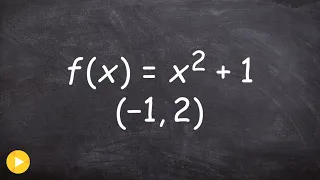
How to determine the absolute max min of a function on an open interval

From playlist Extreme Value Theorem of Functions

Phase Transition in an Ising Model without Detailed Balance by Chandan Dasgupta

DISCUSSION MEETING INDIAN STATISTICAL PHYSICS COMMUNITY MEETING ORGANIZERS Ranjini Bandyopadhyay, Abhishek Dhar, Kavita Jain, Rahul Pandit, Sanjib Sabhapandit, Samriddhi Sankar Ray and Prerna Sharma DATE: 14 February 2019 to 16 February 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalo

From playlist Indian Statistical Physics Community Meeting 2019

Phase Transitions: Diversity in dynamics by Subir Das

Program Entropy, Information and Order in Soft Matter ORGANIZERS Bulbul Chakraborty, Pinaki Chaudhuri, Chandan Dasgupta, Marjolein Dijkstra, Smarajit Karmakar, Vijaykumar Krishnamurthy, Jorge Kurchan, Madan Rao, Srikanth Sastry and Francesco Sciortino DATE & TIME 27 August 2018 to

From playlist Entropy, Information and Order in Soft Matter

Melting of three-sublattice and easy-axis antiferromagnets on triangular and kagome lattices

New questions in quantum field theory from condensed matter theory Talk Title : Melting of threesublattice order in easyaxis antiferromagnets on triangular and kagome lattices by Kedar Damle URL: http://www.icts.res.in/discussion_meeting/qft2015/ Description:- The last couple of decade

From playlist New questions in quantum field theory from condensed matter theory

The Role of Symmetry in Phase Transitions - Tom Spencer

Tom Spencer Professor, School of Mathematics, Institute for Advanced Study January 23, 2012 This talk will review some theorems and conjectures about phase transitions of interacting spin systems in statistical mechanics. A phase transition may be thought of as a change in a typical spin c

From playlist Mathematics

Daniel Fisher - Random quantum Ising spin chains

Random transfer field Ising spin chains are a prototypical example of the interplay between quenched randomness and quantum fluctuations. An approximate real-space renormalization group analysis that becomes exact near the phase zero-temperature phase transition will be presented. Scalin

From playlist 100…(102!) Years of the Ising Model

Exactly solved models by R. Rajesh

DATES Friday 01 Jul, 2016 - Friday 15 Jul, 2016 VENUE Ramanujan Lecture Hall, ICTS Bangalore This advanced level school is the seventh in the series. The school is being jointly organised by the International Centre for Theoretical Sciences (ICTS) and the Raman Research Institute (RRI). T

From playlist Bangalore School On Statistical Physics - VII

Critical Values of Functions (2 of 2: Odd and Even Correspondence in derivatives and primitives)

More resources available at www.misterwootube.com

From playlist Further Work with Functions (related content)

Supersymmetry, Dimensional Reduction and Avalanches in Random-field Models by Gilles Tarjus

DISCUSSION MEETING : CELEBRATING THE SCIENCE OF GIORGIO PARISI (ONLINE) ORGANIZERS : Chandan Dasgupta (ICTS-TIFR, India), Abhishek Dhar (ICTS-TIFR, India), Smarajit Karmakar (TIFR-Hyderabad, India) and Samriddhi Sankar Ray (ICTS-TIFR, India) DATE : 15 December 2021 to 17 December 2021 VE

From playlist Celebrating the Science of Giorgio Parisi (ONLINE)

2020 Theory Winter School: Srinivas Raghu

Topic: Boson-ferimon duality in strongly coupled field theories For more information on the 2020 Theory Winter School: https://nationalmaglab.org/news-events/events/for-scientists/winter-theory-school

From playlist 2020 Theory Winter School

Finding Critical Numbers Example 1

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Finding Critical Numbers Example 1. We find the critical numbers of f(x) = sin^2x + cosx on (0, 2pi).

From playlist Calculus

Andrew JAMES - Truncated spectrum approaches for 2D many-body quantum systems

https://indico.math.cnrs.fr/event/2435/

From playlist Workshop “Hamiltonian methods in strongly coupled Quantum Field Theory”

Ising critical exponents

Related pages