
Integration 7 Integrating the Product of Functions Part 2 Example 1
Working through an example of the reverse of the product rule for integration.
From playlist Integration

Integration 7 Integrating the Product of Functions Part 2 Example 2
Working through an example using the reverse product rule for integration.
From playlist Integration

Ex: Integration by Parts Involving a Trig and Linear Function (x*cos(4x))
This video provides an example of integration by parts. The integrand is a product of a linear function and a trigonometric function. Site: http://mathispower4u.com
From playlist Integration by Parts
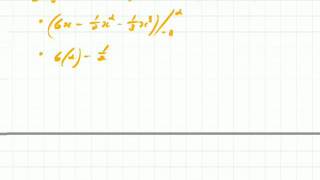
Integration 4 The Definite Integral Part 3 Example 1
An example using the definite integral.
From playlist Integration

Integration 4 The Definite Integral Part 2
Working through an example of the definite integral
From playlist Integration

Integration 1 Riemann Sums Part 1 - YouTube sharing.mov
Introduction to Riemann Sums
From playlist Integration

Integration 4 The Definite Integral Part 3 Example 3
Working through another example using the definite integral.
From playlist Integration

Integration by Parts (After Integration by Parts Basics)
These examples are a little more involved then the Integration by Part - The Basics http://mathispower4u.wordpress.com/
From playlist Integration Intro
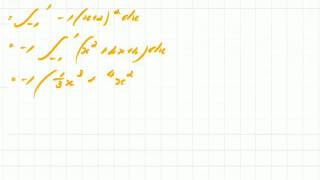
Integration 4 The Definite Integral Part 3 Example 4
Working through another example using the definite integral.
From playlist Integration

Volterra integral operators and generalized Reynolds algebras We study algebraic structures underlying Volterra integral operators, in particular the operator identities satisfied by such operators. While the operator satisfies the Rota-Baxter identity when the kernel of the operator only
From playlist DART X

Markus Rosenkranz Talk 1 7/7/14 Part 3
Title: Integro-Differential Polynomials and Free Integro-Differential Algebras
From playlist Spring 2014

Pre-recorded lecture 6: Constant normal forms, nilpotent Nijenhuis operators and Thompson theorem
MATRIX-SMRI Symposium: Nijenhuis Geometry and integrable systems Pre-recorded lecture: These lectures were recorded as part of a cooperation between the Chinese-Russian Mathematical Center (Beijing) and the Moscow Center of Fundamental and Applied Mathematics (Moscow). Nijenhuis Geomet
From playlist MATRIX-SMRI Symposium: Nijenhuis Geometry companion lectures (Sino-Russian Mathematical Centre)

Yang Liu: Hypergeometric Functions and Heat Coefficients on Noncommutative Tori
Talk by Yang Liu in Global Noncommutative Geometry Seminar (Americas) https://globalncgseminar.org/talks/hypergeometric-functions-and-heat-coefficients-on-noncommutative-tori/ on April 16, 2021.
From playlist Global Noncommutative Geometry Seminar (Americas)

Quantum Physics Full Course | Quantum Mechanics Course
Quantum physics also known as Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all #quantum #physics including quantum chemistry, quantum field theory
From playlist Quantum Mechanics

Sergey Yurkevich - Creative Telescoping for the Canham model in genus 1
The algorithmic method of Creative Telescoping turns out to be an extremely use- ful tool in experimental mathematics, when dealing with concrete mathematical problems. As striking examples, it can be used to compute and prove automati- cally: a recurrence satisfied by any binomial sum (li
From playlist Combinatorics and Arithmetic for Physics: Special Days 2022

Elmar Schrohe: Fourier integral operators on manifolds with boundary and ...
Full Title: Fourier integral operators on manifolds with boundary and the Atiyah-Weinstein index theorem The lecture was held within the framework of the Hausdorff Trimester Program Non-commutative Geometry and its Applications. (18.12.2014)
From playlist HIM Lectures: Trimester Program "Non-commutative Geometry and its Applications"

Annemarie Luger: Herglotz-Nevanlinna functions: realizations and generalizations
CONFERENCE Recorded during the meeting " Herglotz-Nevanlinna Functions and their Applications to Dispersive Systems and Composite Materials " the May 23, 2022 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video a
From playlist Analysis and its Applications

Expectation values of operators
MIT 8.04 Quantum Physics I, Spring 2016 View the complete course: http://ocw.mit.edu/8-04S16 Instructor: Barton Zwiebach License: Creative Commons BY-NC-SA More information at http://ocw.mit.edu/terms More courses at http://ocw.mit.edu
From playlist MIT 8.04 Quantum Physics I, Spring 2016

What is Integration by Parts - How to do Integration by Parts
This tutorial demonstrates how to do integration by parts. Join this channel to get access to perks: https://www.youtube.com/channel/UCn2SbZWi4yTkmPUj5wnbfoA/join :)
From playlist Random Math Videos
