
What is an Injective Function? Definition and Explanation
An explanation to help understand what it means for a function to be injective, also known as one-to-one. The definition of an injection leads us to some important properties of injective functions! Subscribe to see more new math videos! Music: OcularNebula - The Lopez
From playlist Functions

Abstract Algebra | Injective Functions
We give the definition of an injective function, an outline of proving that a given function is injective, and a few examples. http://www.michael-penn.net http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

The Composition of Injective(one-to-one) Functions is Injective Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proof that the composition of injective(one-to-one) functions is also injective(one-to-one)
From playlist Proofs

Definition of an Injective Function and Sample Proof
We define what it means for a function to be injective and do a simple proof where we show a specific function is injective. Injective functions are also called one-to-one functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear https://amzn.to/3BFvcxp (these are my affil
From playlist Injective, Surjective, and Bijective Functions

How to Prove a Function is Injective(one-to-one) Using the Definition
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys How to prove a function is injective. Injective functions are also called one-to-one functions. This is a short video focusing on the proof.
From playlist Proofs

The Definition of an Injective(One to One) Function and Explanation
The Definition of an Injective(One to One) Function and Explanation
From playlist Functions, Sets, and Relations

Proof that if g o f is Injective(one-to-one) then f is Injective(one-to-one)
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proof that if g o f is Injective(one-to-one) then f is Injective(one-to-one). Given two functions f : A to B and g: B to C, we prove that if the composition g o f: A to C is an injective function then f is also an injective function
From playlist Proofs

Injective, Surjective and Bijective Functions (continued)
This video is the second part of an introduction to the basic concepts of functions. It looks at the different ways of representing injective, surjective and bijective functions. Along the way I describe a neat way to arrive at the graphical representation of a function.
From playlist Foundational Math
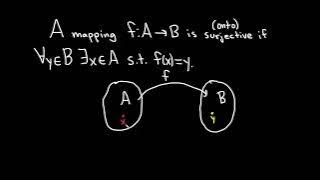
Definition of a Surjective Function and a Function that is NOT Surjective
We define what it means for a function to be surjective and explain the intuition behind the definition. We then do an example where we show a function is not surjective. Surjective functions are also called onto functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear ht
From playlist Injective, Surjective, and Bijective Functions

How Mass Production Shapes Our Weekends | Making The Goods (Part 1 of 2) | Spark
Making The Goods is a documentary about the technology of manufacturing some of our favourite weekend items. No weekend away is complete without your sleeping bag, BBQ or snacks. We go behind the scenes, inside factories, and show how these things are made; from the raw materials, to the f
From playlist Spark Top Docs

Gorenstein Rings In Local Algebra by Srikanth Iyengar
PROGRAM DUALITIES IN TOPOLOGY AND ALGEBRA (ONLINE) ORGANIZERS: Samik Basu (ISI Kolkata, India), Anita Naolekar (ISI Bangalore, India) and Rekha Santhanam (IIT Mumbai, India) DATE & TIME: 01 February 2021 to 13 February 2021 VENUE: Online Duality phenomena are ubiquitous in mathematics
From playlist Dualities in Topology and Algebra (Online)

Daniel Groves: Homomorphisms to 3-manifold groups and other families
Abstract: We are interested in the structure of the set of homomorphisms from a fixed (but arbitrary) finitely generated group G to the groups in some fixed family (such as the family of 3-manifold groups). I will explain what one might hope to say in different situations, and explain some
From playlist Topology

Lauren Williams - Combinatorics of the amplituhedron
The amplituhedron is the image of the positive Grassmannian under a map in- duced by a totally positive matrix. It was introduced by Arkani-Hamed and Trnka to compute scattering amplitudes in N=4 super Yang Mills. I’ll give a gentle introduction to the amplituhedron, surveying its connecti
From playlist Combinatorics and Arithmetic for Physics: Special Days 2022

Johnathan Bush (11/5/21): Maps of Čech and Vietoris–Rips complexes into euclidean spaces
We say a continuous injective map from a topological space to k-dimensional euclidean space is simplex-preserving if the image of each set of at most k+1 distinct points is affinely independent. We will describe how simplex-preserving maps can be useful in the study of Čech and Vietoris–Ri
From playlist Vietoris-Rips Seminar

Yuan-Pin Lee - Introduction to Gromov-Witten theory (Part 1)
In these lectures, Gromov{Witten theory will be introduced, assuming only basic moduli theory covered in the rst week of the School. Then the Crepant Transformation Conjecture will be explained. Some examples, with emphasis on the projective/global cases, will be given. Note: The construct
From playlist École d’été 2011 - Modules de courbes et théorie de Gromov-Witten

Johan Alm: Brown's dihedral moduli space and freedom of the gravity operad
Abstract: Ezra Getzler's gravity cooperad is formed by the degree-shifted cohomology groups of the open moduli spaces M_{0,n}. Francis Brown introduced partial compactifications of these moduli spaces, denoted M_{0,n}^δ. We prove that the (nonsymmetric) gravity cooperad is cofreely cogener
From playlist HIM Lectures: Junior Trimester Program "Topology"

Questions on Weak Gravity Conjecture by Chethan Krishnan
Bangalore Area Strings Meeting - 2017 TIME : 31 July 2017 to 02 August 2017 VENUE:Madhava Lecture Hall, ICTS Bangalore Bengaluru now has a large group of string theorists, with 9 faculty members in the area, between ICTS and IISc. This is apart from a large group of postdocs and graduate
From playlist Bangalore Area Strings Meeting - 2017

Facundo Mémoli: Vietoris-Rips Persistent Homology, Injective Metric Spaces, and The Filling Radius
Title: Vietoris-Rips Persistent Homology, Injective Metric Spaces, and The Filling Radius Abstract: The persistent homology induced by the Vietoris-Rips simplicial filtration is a standard method for capturing topological information from metric spaces. We consider a different, more geome
From playlist Vietoris-Rips Seminar

Injective(one-to-one), Surjective(onto), Bijective Functions Explained Intuitively
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys A nice way to think about injective(one-to-one), surjective(onto), and bijective functions.
From playlist Functions, Sets, and Relations
