Ineffable cardinal

Large cardinals

In the mathematics of transfinite numbers, an ineffable cardinal is a certain kind of large cardinal number, introduced by . In the following definitions, will always be a regular uncountable cardinal number. A cardinal number is called almost ineffable if for every (where is the powerset of ) with the property that is a subset of for all ordinals , there is a subset of having cardinality and homogeneous for , in the sense that for any in , . A cardinal number is called ineffable if for every binary-valued function , there is a stationary subset of on which is homogeneous: that is, either maps all unordered pairs of elements drawn from that subset to zero, or it maps all such unordered pairs to one. An equivalent formulation is that a cardinal is ineffable if for every sequence ⟨Aα : α ∈ κ⟩ such that each Aα ⊆ α, there is A ⊆ κ such that {α ∈ κ : A ∩ α = Aα} is stationary in κ. More generally, is called -ineffable (for a positive integer ) if for every there is a stationary subset of on which is -homogeneous (takes the same value for all unordered -tuples drawn from the subset). Thus, it is ineffable if and only if it is 2-ineffable. A totally ineffable cardinal is a cardinal that is -ineffable for every . If is -ineffable, then the set of -ineffable cardinals below is a stationary subset of . Every n-ineffable cardinal is n-almost ineffable (with set of n-almost ineffable below it stationary), and every n-almost ineffable is n-subtle (with set of n-subtle below it stationary). The least n-subtle cardinal is not even weakly compact (and unlike ineffable cardinals, the least n-almost ineffable is -describable), but n-1-ineffable cardinals are stationary below every n-subtle cardinal. A cardinal κ is completely ineffable if there is a non-empty such that- every is stationary- for every and , there is homogeneous for f with . Using any finite n > 1 in place of 2 would lead to the same definition, so completely ineffable cardinals are totally ineffable (and have greater consistency strength). Completely ineffable cardinals are -indescribable for every n, but the property of being completely ineffable is . The consistency strength of completely ineffable is below that of 1-iterable cardinals, which in turn is below remarkable cardinals, which in turn is below ω-Erdős cardinals. A list of large cardinal axioms by consistency strength is available here. (Wikipedia).

What is an Injective Function? Definition and Explanation

An explanation to help understand what it means for a function to be injective, also known as one-to-one. The definition of an injection leads us to some important properties of injective functions! Subscribe to see more new math videos! Music: OcularNebula - The Lopez

From playlist Functions

The Definition of an Injective(One to One) Function and Explanation

From playlist Functions, Sets, and Relations

Sandra Müller: Lower bounds for the perfect set property at weakly compact cardinals

By the Cantor-Bendixson theorem, subtrees of the binary tree on $\omega$ satisfy a dichotomy - either the tree has countably many branches or there is a perfect subtree (and in particular, the tree has continuum manybranches, regardless of the size of the continuum). We generalize this to

From playlist Logic and Foundations

Math 131 Fall 2018 092118 Cardinality

Recall definitions: injective, surjective, bijective, cardinality. Definitions: finite, countable, at most countable, uncountable, sequence. Remark: a 1-1 correspondence with the natural numbers is the same thing as a bijective sequence. Theorem: Every infinite subset of a countable set

From playlist Course 7: (Rudin's) Principles of Mathematical Analysis (Fall 2018)

How to Prove a Function is Injective(one-to-one) Using the Definition

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys How to prove a function is injective. Injective functions are also called one-to-one functions. This is a short video focusing on the proof.

From playlist Proofs

The Composition of Injective(one-to-one) Functions is Injective Proof

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proof that the composition of injective(one-to-one) functions is also injective(one-to-one)

From playlist Proofs

Definition of an Injective Function and Sample Proof

We define what it means for a function to be injective and do a simple proof where we show a specific function is injective. Injective functions are also called one-to-one functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear https://amzn.to/3BFvcxp (these are my affil

From playlist Injective, Surjective, and Bijective Functions

Jason Silva's Origin Story | Origins: The Journey of Humankind

Origins host Jason Silva talks about how childhood curiosity led him to pursue a career in communicating seemingly ineffable ideas. ➡ Subscribe: http://bit.ly/NatGeoSubscribe ➡ Watch all clips of Origins: The Journey of Humankind here: http://bit.ly/WatchNGOrigins About Origins: The Journ

From playlist Exploration | National Geographic

8. Inferno XXVI, XXVII, XXVIII

Dante in Translation (ITAL 310) Professor Mazzotta begins this lecture by recapitulating the ambivalent nature of Ulysses' sin and its relevance to Dante's poetic project. Inferno XXVII is then read in conjunction with the preceding canto. The antithetical relationship between Dante's f

From playlist Dante in Translation with Giuseppe Mazzotta

Introduction to the Cardinality of Sets and a Countability Proof

Introduction to Cardinality, Finite Sets, Infinite Sets, Countable Sets, and a Countability Proof - Definition of Cardinality. Two sets A, B have the same cardinality if there is a bijection between them. - Definition of finite and infinite sets. - Definition of a cardinal number. - Discu

From playlist Set Theory

Daniel C. Dennett - What is Consciousness?

Consciousness is what we can know best and explain least. It is the inner subjective experience of what it feels like to see red or smell garlic or hear Beethoven. Consciousness has intrigued and baffled philosophers. To begin, we must define and describe consciousness. What to include in

From playlist What is Consciousness? - CTT Interview Series

Wittgenstein - The Unsayable & Limits of Thought

In this clip, Ray Monk, Barry Smith, and Marie McGinn discuss the early Wittgenstein's thought in regards to the famous last proposition of the Tractatus: "Whereof one cannot speak, thereof one must be silent." This clip comes from an episode of the podcast In Our Time a few years back. Fo

From playlist Wittgenstein

Richard Rorty on Purity

A clip of Richard Rorty discussing the notion of purity. This comes from the documentary "Of Beauty and Consolation". More Short Clips: https://www.youtube.com/playlist?list=PLhP9EhPApKE8v8UVlc7JuuNHwvhkaOvzc #Philosophy #Rorty #Pragmatism

From playlist Shorter Clips & Videos - Philosophy Overdose

Proof that if g o f is Injective(one-to-one) then f is Injective(one-to-one)

Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Proof that if g o f is Injective(one-to-one) then f is Injective(one-to-one). Given two functions f : A to B and g: B to C, we prove that if the composition g o f: A to C is an injective function then f is also an injective function

From playlist Proofs

Cultural Literacy and Religions of the World

Learn more about this course and start your FREE trial here: https://wondrium.com/youtube/lp/t2/generic?utm_source=Video&utm_medium=Youtube&utm_campaign=149628 When does the Jewish Sabbath begin? Who are Vishnu and Shiva? What are Buddhism's Four Noble Truths? What are the Five Pillars of

From playlist Latest Uploads

Is Your Red The Same as My Red?

Subscribe to Vsauce: http://bit.ly/POIaN7 Follow Michael Stevens: http://www.twitter.com/tweetsauce http://facebook.com/VsauceGaming All music by Jake Chudnow: http://www.youtube.com/jakechudnow Tommy Edison (Blind guy on YouTube): http://bit.ly/rjyX7q Color Blindness: http://www.colou

From playlist DOT.

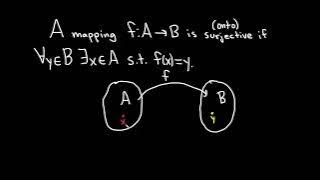
Definition of a Surjective Function and a Function that is NOT Surjective

We define what it means for a function to be surjective and explain the intuition behind the definition. We then do an example where we show a function is not surjective. Surjective functions are also called onto functions. Useful Math Supplies https://amzn.to/3Y5TGcv My Recording Gear ht

From playlist Injective, Surjective, and Bijective Functions

The “heroic dose” of psychedelics, according to Johns Hopkins | Dr. Matthew Johnson

How a ‘heroic dose’ of psychedelics can be therapeutic, explained by a Johns Hopkins professor. Subscribe to Big Think on YouTube ► https://www.youtube.com/channel/UCvQECJukTDE2i6aCoMnS-Vg?sub_confirmation=1 Up next, Psychedelics: The scientific renaissance of mind-altering drugs ► https

From playlist Psychedelics & performance drugs | Big Think

Michael Pollan on writing: What illuminates a story?

New videos DAILY: https://bigth.ink Join Big Think Edge for exclusive video lessons from top thinkers and doers: https://bigth.ink/Edge ---------------------------------------------------------------------------------- When it comes to writing a story, it's important to find a way to ha

From playlist Writing tips from the experts | Big Think

Transcendental numbers powered by Cantor's infinities

In today's video the Mathologer sets out to give an introduction to the notoriously hard topic of transcendental numbers that is both in depth and accessible to anybody with a bit of common sense. Find out how Georg Cantor's infinities can be used in a very simple and off the beaten track

From playlist Recent videos

Ineffable cardinal

Related pages