
A02 Independence of the solution set
The independence of a linear system. How to make sure that a set of solutions are not constant multiples of each other.
From playlist A Second Course in Differential Equations

Further examination of independence
From playlist Unit 5 Probability A: Basic Probability

More Help with Independence Part 2Indep FE pt 2
More insight into the probability concept of independence
From playlist Unit 5 Probability A: Basic Probability

(0:00) Independence of two events (4:12) (Mutual) Independence of multiple events (9:30) Conditional Independence of two events A playlist of the Probability Primer series is available here: http://www.youtube.com/view_play_list?p=17567A1A3F5DB5E4
From playlist Probability Theory

America the Story of Us: Declaration of Independence | History
The Declaration of Independence marks the first such document declaring the equality of men. Own America: The Story of Us on DVD or Blu-ray! http://www.shophistorystore.com/ HISTORY®, now reaching more than 98 million homes, is the leading destination for award-winning original series and
From playlist Presidential History
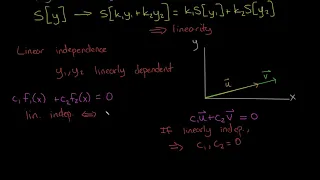
Differential Equations: Linear Independence
Linear independence is a core idea from Linear Algebra. Surprisingly, it's also important in differential equations. This video is the second precursor to our discussion of homogeneous differential equations.
From playlist Differential Equations
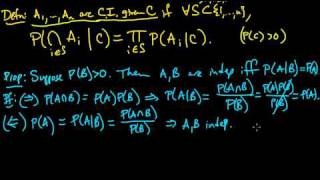
(PP 2.3) Independence (continued)
(0:00) (Mutual) Independence of an infinite sequence of events. (1:55) Conditional Independence of multiple events. (3:28) Relationship between independence and conditional probability. (7:23) Example illustrating the relationships between independence, pairwise independence, mutu
From playlist Probability Theory

Linear Independence Problems - Using the Definition
In this video, I review the definition of linear independence and work through some practice problems using the definition. To learn more about linear independence, check out this lecture in my Linear Algebra Lectures video series: https://youtu.be/KE7xHcwfxzQ
From playlist Linear Algebra Lectures

Microservices: A Retrospective
SOA has been around for decades, and its latest iteration - microservices - for a while now. Just five years ago microservices were hip, dominating the agenda at conferences; now we almost take them for granted. With microservice-focused conference talks losing steam, the time is ripe to c
From playlist Microservices

W. Zheng - Compatible systems along the boundary
A theorem of Deligne says that compatible systems of l-adic sheaves on a smooth curve over a finite field are compatible along the boundary. I will present an extension of Deligne's theorem to schemes of finite type over the ring of integers of a local field, based on Gabber's theorem on c
From playlist Arithmetic and Algebraic Geometry: A conference in honor of Ofer Gabber on the occasion of his 60th birthday

MIT RES.6-012 Introduction to Probability, Spring 2018 View the complete course: https://ocw.mit.edu/RES-6-012S18 Instructor: John Tsitsiklis License: Creative Commons BY-NC-SA More information at https://ocw.mit.edu/terms More courses at https://ocw.mit.edu
From playlist MIT RES.6-012 Introduction to Probability, Spring 2018

29 - Determining linear independence
Algebra 1M - international Course no. 104016 Dr. Aviv Censor Technion - International school of engineering
From playlist Algebra 1M

Time-dependent non-Hermitian systems a status update by Andreas Fring
DATE: 04 June 2018 to 13 June 2018 VENUE:Ramanujan Lecture Hall, ICTS Bangalore Non-Hermitian Physics-"Pseudo-Hermitian Hamiltonians in Quantum Physics (PHHQP) XVIII" is the 18th meeting in the series that is being held over the years in Quantum Physics. The scope of the program on Non-H
From playlist Non-Hermitian Physics - PHHQP XVIII

(0.3.101) Exercise 0.3.101: Classifying Differential Equations
This video explains how to classify differential equations based upon their properties https://mathispower4u.com
From playlist Differential Equations: Complete Set of Course Videos

Math 060 Linear Algebra 10 092914: Vector Space Bases
Basis; dimension; cardinality of a linearly independent set cannot exceed that of a spanning set; if a set has the same cardinality as the dimension of the vector space, then linear independence is equivalent to that set spanning the vector space; any linear independent set can be extended
From playlist Course 4: Linear Algebra

Mod-01 Lec-7 Physical Properties of Crystals (Continued)
Condensed Matter Physics by Prof. G. Rangarajan, Department of Physics, IIT Madras. For more details on NPTEL visit http://nptel.iitm.ac.in
From playlist NPTEL: Condensed Matter Physics - CosmoLearning.com Physics Course

Controllability of a Linear System: The Controllability Matrix and the PBH Test
In this video we explore controllability of a linear system. We discuss two methods to test for controllability, the controllability matrix as well as the PBH test. Topics and time stamps: 0:00 – Introduction and definition. 1:04 – Controllability of a dog. 3:48 – Controllability matrix.
From playlist Control Theory

23 Algebraic system isomorphism
Isomorphic algebraic systems are systems in which there is a mapping from one to the other that is a one-to-one correspondence, with all relations and operations preserved in the correspondence.
From playlist Abstract algebra

