
Python - strings and collections (part 1 of 3)
Strings and collections in the Python language. Part of a larger series at codeschool.org
From playlist Python strings and collections
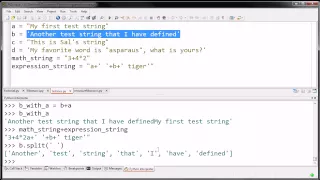
Experimenting and seeing what we can do with strings
From playlist Computer Science

Strings in Python - Advanced Python 05 - Programming Tutorial
Strings in Python - Advanced Python 05 - Programming Tutorial In this Python Advanced Tutorial, we will be learning about Strings in Python. A String is an ordered, and immutable collection data type that is used for text representation, and it's one of the most used data types in Python.
From playlist Advanced Python - Complete Course

Strings In Python | Python Strings | What Are Strings In Python? | Python For Beginners |Simplilearn
This video on Strings in Python will help you create strings in Python. You will learn about string indexing. You will also explore the various inbuilt functions in Python that makes it easier to work with strings, concatenate strings and use the format method for doing the same. Below to
From playlist Python For Beginners 🔥[2022 Updated]

More videos like this online at http://www.theurbanpenguin.com We do quite a lot in this video so if you are new to Java you will get a lot out of this. First we revisit StringBuilder and the reverse method. Then looking at how we can assign non-string values to strings with concatenation
From playlist Java

From playlist Week 4 2015 Shorts

Sequences: Introduction to Solving Recurrence Relations
This video introduces solving recurrence relations by the methods of inspection, telescoping, and characteristic root technique. mathispower4u.com
From playlist Sequences (Discrete Math)

Verónica Becher: Independence of normal words
Abstract : Recall that normality is a elementary form of randomness: an infinite word is normal to a given alphabet if all blocks of symbols of the same length occur in the word with the same asymptotic frequency. We consider a notion of independence on pairs of infinite words formalising
From playlist Logic and Foundations

Recursively Defined Sets - An Intro
Recursively defined sets are an important concept in mathematics, computer science, and other fields because they provide a framework for defining complex objects or structures in a simple, iterative way. By starting with a few basic objects and applying a set of rules repeatedly, we can g
From playlist All Things Recursive - with Math and CS Perspective

How to build a fluid clock - Theodore Dimitrios Drivas
Short Talks by Postdoctoral Members Topic: How to build a fluid clock Speaker: Theodore Dimitrios Drivas Affiliation: Member, School of Mathematics Date: February 01, 2022
From playlist Mathematics

Jessica Purcell - Lecture 1 - Hyperbolic knots and alternating knots
Jessica Purcell, Monash University Title: Hyperbolic knots and alternating knots Hyperbolic geometry has been used since around the mid-1970s to study knot theory, but it can be difficult to relate geometry of knots to a diagram of a knot. However, many results from the 1980s and beyond s
From playlist 39th Annual Geometric Topology Workshop (Online), June 6-8, 2022

Jintian Zhu - Incompressible hypersurface, positive scalar curvature and positive mass theorem
In this talk, I will introduce a positive mass theorem for asymptotically flat manifolds with fibers (like ALF and ALG manifolds) under an additional but necessary incompressible condition. I will also make a discussion on its connection with surgery theory as well as quasi-local mass and
From playlist Not Only Scalar Curvature Seminar

MFEM Workshop 2021 | An Adaptive, Scalable Fully Implicit Resistive MHD Solver
The LLNL-led MFEM (Modular Finite Element Methods) project provides high-order mathematical calculations for large-scale scientific simulations. The project’s first community workshop was held virtually on October 20, 2021, with participants around the world. Learn more about MFEM at https
From playlist MFEM Community Workshop 2021

The Archimedes Principle | Szydlo's At Home Science
Andrew explores the well know but perhaps not so well understood Archimedes principle. We start off in ancient Sicily for a surprising dip in the bath with Archimedes, followed by a variety of experiments and demonstrations back in Andrew's basement lab. the properties of both liquids and
From playlist Shedloads of Szydlo

From playlist Week 2 2014

Jean-Claude Saut : Lagrange and water waves
he most important works of the young Lagrange were two very learned memoirs on sound and its propagation. In a tour de force of mathematical analysis, he solved the relevant partial differential equations in a novel manner and he applied the solutions to a number of acoustic problems. Alth
From playlist Lagrange Days at CIRM

Dual cascade, dissipation mechanisms and finite temperature effects by Marc Brachet
Turbulence from Angstroms to light years DATE:20 January 2018 to 25 January 2018 VENUE:Ramanujan Lecture Hall, ICTS, Bangalore The study of turbulent fluid flow has always been of immense scientific appeal to engineers, physicists and mathematicians because it plays an important role acr
From playlist Turbulence from Angstroms to light years

Michael Atiyah: Poincaré conjecture, Hodge conjecture, Yang-Mills, Navier-Stokes [2000]
Millennium Meeting These videos document the Institute's landmark Paris millennium event which took place on May 24-25, 2000, at the Collège de France. On this occasion, CMI unveiled the "Millennium Prize Problems," seven mathematical quandaries that have long resisted solution. The announ
From playlist Number Theory

Giray Ökten: Number sequences for simulation - lecture 1
After an overview of some approaches to define random sequences, we will discuss pseudorandom sequences and low-discrepancy sequences. Applications to numerical integration, Koksma-Hlawka inequality, and Niederreiter’s uniform point sets will be discussed. We will then present randomized q
From playlist Probability and Statistics

In physics, string theory is a theoretical framework in which the point-like particles of particle physics are replaced by one-dimensional objects called strings. String theory describes how these strings propagate through space and interact with each other. On distance scales larger than
From playlist Physics