
Imaginary Numbers, Functions of Complex Variables: 3D animations.
Visualization explaining imaginary numbers and functions of complex variables. Includes exponentials (Euler’s Formula) and the sine and cosine of complex numbers.
From playlist Physics

Imaginary numbers are any numbers that include the imaginary number i. A mix of imaginary and real numbers gives you what’s called a complex number. The primary reason we use imaginary numbers is to give us a way to find the root (radical) of a negative number. There’s no way to use real
From playlist Popular Questions

Imaginary Numbers Are Real [Part 11: Wandering in 4 Dimensions]
More information and resources: http://www.welchlabs.com Supporting Code: https://github.com/stephencwelch/Imaginary-Numbers-Are-Real Imaginary numbers are not some wild invention, they are the deep and natural result of extending our number system. Imaginary numbers are all about the di
From playlist Imaginary Numbers are Real
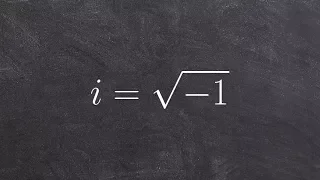
Tutorial - What is an imaginary number
http://www.freemathvideos.com In this video playlist you will learn everything you need to know with complex and imaginary numbers
From playlist Complex Numbers

Imaginary Numbers Are Real [Part 10: Complex Functions]
Supporting Code: https://github.com/stephencwelch/Imaginary-Numbers-Are-Real More information and resources: http://www.welchlabs.com Imaginary numbers are not some wild invention, they are the deep and natural result of extending our number system. Imaginary numbers are all about the di
From playlist Imaginary Numbers are Real

Imaginary Numbers Are Real [Part 1: Introduction]
For early access to new videos and other perks: https://www.patreon.com/welchlabs Want to learn more or teach this series? Check out the Imaginary Numbers are Real Workbook: http://www.welchlabs.com/resources. Imaginary numbers are not some wild invention, they are the deep and natural
From playlist Imaginary Numbers are Real
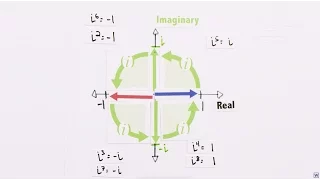
Imaginary Numbers Are Real [Part 5: Numbers are Two Dimensional]
More information and resources: http://www.welchlabs.com Imaginary numbers are not some wild invention, they are the deep and natural result of extending our number system. Imaginary numbers are all about the discovery of numbers existing not in one dimension along the number line, but in
From playlist Imaginary Numbers are Real

How Imaginary Numbers Make Real Physics Easier to Understand
Go to Squarespace.com for a free trial, and when you’re ready to launch, go to http://www.squarespace.com/parthg to save 10% off your first purchase of a website or domain. #imaginarynumber #complexnumbers #physics In this video, we'll look at the basics of complex and imaginary numbers,
From playlist Quantum Physics by Parth G

Imaginary Numbers Are Real [Part 9: Closure]
More information and resources: http://www.welchlabs.com Imaginary numbers are not some wild invention, they are the deep and natural result of extending our number system. Imaginary numbers are all about the discovery of numbers existing not in one dimension along the number line, but in
From playlist Imaginary Numbers are Real
Imaginaries in separably closed valued fields
From playlist Spring 2019 Kolchin Seminar

The Fundamental Domain | The Geometry of SL(2,Z), Section 1.2
The fundamental domain for SL(2,Z) on the complex upper half plane is described, with proof. We also derive the stabilizers of the action, and provide generators for SL(2,Z). My Twitter: https://twitter.com/KristapsBalodi3 Description of the Fundamental Domain:(0:00) Statement of Main T
From playlist The Geometry of SL(2,Z)

Hyperbolic geometry, the modular group and Diophantine (Lecture - 01) by Shrikrishna G Dani
Geometry, Groups and Dynamics (GGD) - 2017 DATE: 06 November 2017 to 24 November 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The program focuses on geometry, dynamical systems and group actions. Topics are chosen to cover the modern aspects of these areas in which research has b
From playlist Geometry, Groups and Dynamics (GGD) - 2017

[ANT07] Units and logarithm space (+ bonus theorems)
There are infinitely many units in Z[√2]. How can we write them down? How can we figure out their multiplicative structure? (Plus, now that we've come this far, a few theorems to make the link between this course and more traditional courses.)
From playlist [ANT] An unorthodox introduction to algebraic number theory

Xevi Guitart : Endomorphism algebras of geometrically split abelian surfaces over Q
CONFERENCE Recording during the thematic meeting : "COUNT, COmputations and their Uses in Number Theory" the February 28, 2023 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Jean Petit Find this video and other talks given by worldwide mathematici
From playlist JEAN MORLET CHAIR

Toward an imaginary Ax-Kochen-Ershov principle - S. Rideau - Workshop 2 - CEB T1 2018
Silvain Rideau (CNRS – Université Paris Diderot) / 09.03.2018 Toward an imaginary Ax-Kochen-Ershov principle. All imaginaries that have been classified in Henselian fields (possibly with operators) have been shown to be geometric in the sense of Haskell-HrushovskiMacpherson. In general,
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

This is part of an online course on intermediate/advanced MATLAB programming skills. The course includes almost 40 hours of video instructions that focus on solving applications-oriented problems in MATLAB. More info here: https://www.udemy.com/master-matlab-through-guided-problem-solving
From playlist Master MATLAB through guided problem-solving

Abstract Algebra | Introduction to Euclidean Domains
We give the definition of a Euclidean domain, provide some examples including the Gaussian Integers Z[i], and prove that every Euclidean domain is a principal ideal domain (PID). Please Subscribe: https://www.youtube.com/michaelpennmath?sub_confirmation=1 Personal Website: http://www.mi
From playlist Abstract Algebra
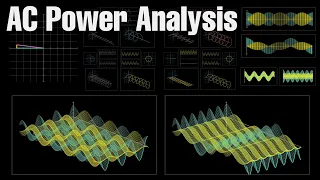
AC Power Analysis: Complex power, Active power, Reactive power, Apparent power, and Power factor
SUBSCRIBE : https://www.youtube.com/c/TheSiGuyEN?sub_confirmation=1 _________________________________ Join this channel to get access to perks: https://www.youtube.com/channel/UCcTgnJE_RKa8-Qzx6lB78lg/join _______________ You can support the future videos : https://www.patreon.com/TheSiGu
From playlist AC Analysis

This video lesson is part of a complete course on neuroscience time series analyses. The full course includes - over 47 hours of video instruction - lots and lots of MATLAB exercises and problem sets - access to a dedicated Q&A forum. You can find out more here: https://www.udemy.
From playlist NEW ANTS #2) Static spectral analysis

Imaginary Numbers Are Real [Part 6: The Complex Plane]
For full problem statement, check out: http://www.welchlabs.com/blog/2015/10/2/imaginary-numbers-are-real-part-6-the-complex-plane More information and resources: http://www.welchlabs.com Imaginary numbers are not some wild invention, they are the deep and natural result of extending our
From playlist Imaginary Numbers are Real