
RNT1.4. Ideals and Quotient Rings
Ring Theory: We define ideals in rings as an analogue of normal subgroups in group theory. We give a correspondence between (two-sided) ideals and kernels of homomorphisms using quotient rings. We also state the First Isomorphism Theorem for Rings and give examples.
From playlist Abstract Algebra

Now that we know what a quotient group is, let's take a look at an example to cement our understanding of the concepts involved.
From playlist Abstract algebra

The idea of a quotient group follows easily from cosets and Lagrange's theorem. In this video, we start with a normal subgroup and develop the idea of a quotient group, by viewing each coset (together with the normal subgroup) as individual mathematical objects in a set. This set, under
From playlist Abstract algebra

Abstract Algebra | The motivation for the definition of an ideal.
Towards the goal of creating a quotient ring, we uncover the defintion of an ideal. http://www.michael-penn.net https://www.researchgate.net/profile/Michael_Penn5 http://www.randolphcollege.edu/mathematics/
From playlist Abstract Algebra

Ideals in Ring Theory (Abstract Algebra)
An ideal of a ring is the similar to a normal subgroup of a group. Using an ideal, you can partition a ring into cosets, and these cosets form a new ring - a "factor ring." (Also called a "quotient ring.") After reviewing normal subgroups, we will show you *why* the definition of an ide
From playlist Abstract Algebra

Fundamentals of Mathematics - Lecture 25: Quotient Maps (Real Projective Line, Modular Arithmetic)
course page - https://www.uvm.edu/~tdupuy/logic/Math52-Fall2017.html videography - Eric Melton, UVM
From playlist Fundamentals of Mathematics
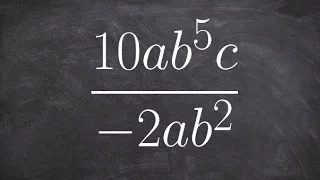
👉 Learn how to simplify expressions using the quotient rule of exponents. The quotient rule of exponents states that the quotient of powers with a common base is equivalent to the power with the common base and an exponent which is the difference of the exponents of the term in the numerat
From playlist Simplify Using the Rules of Exponents | Quotient Rule

Proof: Ideal of a Ring is Proper iff it has no Units | Abstract Algebra
An ideal of a ring with identity is proper if and only if the ideal contains no units of the ring. We prove this result in today's abstract algebra video lesson! Remember that an ideal, I, of a ring, R, is an additive subgroup of I such that for all r in R and x in I, r*x and x*r are also
From playlist Abstract Algebra

I is a Prime Ideal iff R/I is an Integral Domain Proof
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys I is a Prime Ideal iff R/I is an Integral Domain Proof
From playlist Abstract Algebra

Visual Group Theory, Lecture 7.3: Ring homomorphisms
Visual Group Theory, Lecture 7.3: Ring homomorphisms A ring homomorphism is a structure preserving map between rings, which means that f(x+y)=f(x)+f(y) and f(xy)=f(x)f(y) both must hold. The kernel is always a two-sided ideal. There are four isomorphism theorems for rings, which are compl
From playlist Visual Group Theory

RNT2.1. Maximal Ideals and Fields
Ring Theory: We now consider special types of rings. In this part, we define maximal ideals and explore their relation to fields. In addition, we note three ways to construct fields.
From playlist Abstract Algebra

Proof: Prime Ideal iff R/P is Integral Domain; Maximal iff R/M is Field
A very useful theorem in ring theory is the theorem that an ideal P is prime if and only if the quotient R/P is an integral domain (ID). Similarly, an ideal M is maximal if and only if R/M is a field. In this video, we prove both of these statements! Ring & Module Theory playlist: https:/
From playlist Ring & Module Theory

Commutative algebra 17 (Spec R[1/S])
This lecture is part of an online course on commutative algebra, following the book "Commutative algebra with a view toward algebraic geometry" by David Eisenbud. In this lecture we compare the spectrum of R with that of the localization of R at a multiplicative subset S. A examples we di
From playlist Commutative algebra

Visual Group Theory, Lecture 7.2: Ideals, quotient rings, and finite fields
Visual Group Theory, Lecture 7.2: Ideals, quotient rings, and finite fields A left (resp., right) ideal of a ring R is a subring that is invariant under left (resp., right) multiplication. Two-sided ideals are those that are both left and right ideals. This is the analogue of normal subgr
From playlist Visual Group Theory

Abstract Algebra | Maximal and prime ideals.
We prove some classic results involving maximal and prime ideals. Specifically we prove the an ideal P is prime iff R/P is an integral domain. Further, we prove that an ideal M is maximal iff R/M is a field. http://www.michael-penn.net https://www.researchgate.net/profile/Michael_Penn5 ht
From playlist Abstract Algebra
AKPotW: Quotient Rings [Abstract Algebra]
If this video is confusing, be sure to check out our blog for the full solution transcript! https://centerofmathematics.blogspot.com/2018/03/advanced-knowledge-problem-of-week-3-22.html
From playlist Center of Math: Problems of the Week

This lecture is part of an online algebraic geometry course on schemes, based on chapter II of "Algebraic geometry" by Hartshorne. We will review the localization of a ring at a multiplicative subset or prime ideal, and describe what this does to the spectrum of a ring.
From playlist Algebraic geometry II: Schemes

These are some definitions about infinite products. You shouldn't watch this video.
From playlist Riemann Hypothesis

Sarah Reznikoff: Regular ideals and regular inclusions
Talk in Global Noncommutative Geometry Seminar (Europe) on April 20, 2022
From playlist Global Noncommutative Geometry Seminar (Europe)
