Hyperbola 3D Animation | Objective conic hyperbola | Digital Learning
Hyperbola 3D Animation In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other an
From playlist Maths Topics
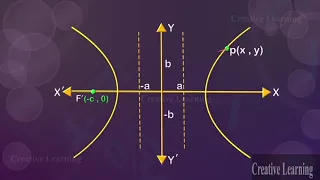
What is the definition of a hyperbola
Learn all about hyperbolas. A hyperbola is a conic section with two fixed points called the foci such that the difference between the distances of any point on the hyperbola from the two foci is equal to the distance between the two foci. Some of the characteristics of a hyperbola includ
From playlist The Hyperbola in Conic Sections

What is the definition of a hyperbola
Learn all about hyperbolas. A hyperbola is a conic section with two fixed points called the foci such that the difference between the distances of any point on the hyperbola from the two foci is equal to the distance between the two foci. Some of the characteristics of a hyperbola includ
From playlist The Hyperbola in Conic Sections

Julien Duval - Kobayashi pseudo-metrics, entire curves and hyperbolicity of algebraic varieties 1/2
An almost complex manifold is hyperbolic if it does not contain any entire curve. We start characterizing hyperbolic compact almost complex manifolds. These are the ones whose holomorphic discs satisfy a linear isoperimetric inequality. Then we prove the almost complex version of the Greee
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications

Julien Duval - Kobayashi pseudo-metrics, entire curves and hyperbolicity of algebraic varieties 2/2
An almost complex manifold is hyperbolic if it does not contain any entire curve. We start characterizing hyperbolic compact almost complex manifolds. These are the ones whose holomorphic discs satisfy a linear isoperimetric inequality. Then we prove the almost complex version of the Greee
From playlist École d’été 2012 - Feuilletages, Courbes pseudoholomorphes, Applications

Noether's works in Topology by Indranil Biswas
DATES: Monday 29 Aug, 2016 - Tuesday 30 Aug, 2016 VENUE: Madhava Lecture Hall, ICTS Bangalore Emmy Noether (1882-1935) is well known for her famous contributions to abstract algebra and theoretical physics. Noether’s mathematical work has been divided into three ”epochs”. In the first (
From playlist The Legacy of Emmy Noether

Jessica Purcell: Structure of hyperbolic manifolds - Lecture 3
Abstract: In these lectures, we will review what it means for a 3-manifold to have a hyperbolic structure, and give tools to show that a manifold is hyperbolic. We will also discuss how to decompose examples of 3-manifolds, such as knot complements, into simpler pieces. We give conditions
From playlist Topology

The circle and projective homogeneous coordinates (cont.) | Universal Hyperbolic Geometry 7b
Universal hyperbolic geometry is based on projective geometry. This video introduces this important subject, which these days is sadly absent from most undergrad/college curriculums. We adopt the 19th century view of a projective space as the space of one-dimensional subspaces of an affine
From playlist Universal Hyperbolic Geometry

Algebra Ch 40: Hyperbolas (1 of 10) What is a Hyperbola?
Visit http://ilectureonline.com for more math and science lectures! To donate: http://www.ilectureonline.com/donate https://www.patreon.com/user?u=3236071 We will learn a hyperbola is a graph that result from meeting the following conditions: 1) |d1-d2|=constant (same number) 2) the grap
From playlist THE "HOW TO" PLAYLIST

Recognising Fractals from a reasonable distance - Logarithmic Distance Estimation Edition.
Recognising Fractals from a reasonable distance - Logarithmic Distance Estimation Edition. Today's lesson features the following fractals, presented at reasonable distances: Aexion Benesi Pine Tree Benesi Pow 2 Benesi Pow 2 Mandelbulb Box Fold Bulb Pow 2 Box Fold Bulb Menger Box Fold Qua
From playlist Nerdy Rodent Uploads!

Emmy Noether’s ideas in Gravity, Black holes and AdS/CFT by Loganayagam
DATES: Monday 29 Aug, 2016 - Tuesday 30 Aug, 2016 VENUE: Madhava Lecture Hall, ICTS Bangalore Emmy Noether (1882-1935) is well known for her famous contributions to abstract algebra and theoretical physics. Noether’s mathematical work has been divided into three ”epochs”. In the first (
From playlist The Legacy of Emmy Noether

Jessica Purcell: Structure of hyperbolic manifolds - Lecture 2
Abstract: In these lectures, we will review what it means for a 3-manifold to have a hyperbolic structure, and give tools to show that a manifold is hyperbolic. We will also discuss how to decompose examples of 3-manifolds, such as knot complements, into simpler pieces. We give conditions
From playlist Topology

Noether's theorems and their growing physical relevance by Joseph Samuel
DATES: Monday 29 Aug, 2016 - Tuesday 30 Aug, 2016 VENUE: Madhava Lecture Hall, ICTS Bangalore Emmy Noether (1882-1935) is well known for her famous contributions to abstract algebra and theoretical physics. Noether’s mathematical work has been divided into three ”epochs”. In the first (
From playlist The Legacy of Emmy Noether

Hypercomplex numbers | Math History | NJ Wildberger
In the 19th century, the geometrical aspect of the complex numbers became generally appreciated, and mathematicians started to look for higher dimensional examples of how arithmetic interacts with geometry. A particularly interesting development is the discovery of quaternions by W. R. H
From playlist MathHistory: A course in the History of Mathematics

Origin and Development of Valuation Theory by Sudesh Khanduja
DATES: Monday 29 Aug, 2016 - Tuesday 30 Aug, 2016 VENUE: Madhava Lecture Hall, ICTS Bangalore Emmy Noether (1882-1935) is well known for her famous contributions to abstract algebra and theoretical physics. Noether’s mathematical work has been divided into three ”epochs”. In the first (
From playlist The Legacy of Emmy Noether

Noether's theorem and particle physics by Rohini Godbole
DATES: Monday 29 Aug, 2016 - Tuesday 30 Aug, 2016 VENUE: Madhava Lecture Hall, ICTS Bangalore Emmy Noether (1882-1935) is well known for her famous contributions to abstract algebra and theoretical physics. Noether’s mathematical work has been divided into three ”epochs”. In the first (
From playlist The Legacy of Emmy Noether

Symmetries and Condensed Matter physics by Subhro Bhattacharya
DATES: Monday 29 Aug, 2016 - Tuesday 30 Aug, 2016 VENUE: Madhava Lecture Hall, ICTS Bangalore Emmy Noether (1882-1935) is well known for her famous contributions to abstract algebra and theoretical physics. Noether’s mathematical work has been divided into three ”epochs”. In the first (
From playlist The Legacy of Emmy Noether

Interplay of symmetries and other integrability quantifiers in finite by Lakhsmanan Muthusamy
DATES: Monday 29 Aug, 2016 - Tuesday 30 Aug, 2016 VENUE: Madhava Lecture Hall, ICTS Bangalore Emmy Noether (1882-1935) is well known for her famous contributions to abstract algebra and theoretical physics. Noether’s mathematical work has been divided into three ”epochs”. In the first (
From playlist The Legacy of Emmy Noether

Emmy Noether in Erlangen and Göttingen by Ravi Rao
DATES: Monday 29 Aug, 2016 - Tuesday 30 Aug, 2016 VENUE: Madhava Lecture Hall, ICTS Bangalore Emmy Noether (1882-1935) is well known for her famous contributions to abstract algebra and theoretical physics. Noether’s mathematical work has been divided into three ”epochs”. In the first (
From playlist The Legacy of Emmy Noether

Jessica Purcell: Structure of hyperbolic manifolds - Lecture 1
Abstract: In these lectures, we will review what it means for a 3-manifold to have a hyperbolic structure, and give tools to show that a manifold is hyperbolic. We will also discuss how to decompose examples of 3-manifolds, such as knot complements, into simpler pieces. We give conditions
From playlist Topology