
Computing homology groups | Algebraic Topology | NJ Wildberger
The definition of the homology groups H_n(X) of a space X, say a simplicial complex, is quite abstract: we consider the complex of abelian groups generated by vertices, edges, 2-dim faces etc, then define boundary maps between them, then take the quotient of kernels mod boundaries at each
From playlist Algebraic Topology

Homomorphisms in abstract algebra
In this video we add some more definition to our toolbox before we go any further in our study into group theory and abstract algebra. The definition at hand is the homomorphism. A homomorphism is a function that maps the elements for one group to another whilst maintaining their structu
From playlist Abstract algebra

Homotopy type theory: working invariantly in homotopy theory -Guillaume Brunerie
Short talks by postdoctoral members Topic: Homotopy type theory: working invariantly in homotopy theory Speaker: Guillaume Brunerie Affiliation: Member, School of Mathematics Date: September 26, 2017 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Introduction to Homotopy Theory- PART 1: UNIVERSAL CONSTRUCTIONS
The goal of this series is to develop homotopy theory from a categorical perspective, alongside the theory of model categories. We do this with the hope of eventually developing stable homotopy theory, a personal goal a passion of mine. I'm going to follow nLab's notes, but I hope to add t
From playlist Introduction to Homotopy Theory

Benjamin Schweinhart (4/3/18): Persistent homology and the upper box dimension
We prove the first results relating persistent homology to a classically defined fractal dimension. Several previous studies have demonstrated an empirical relationship between persistent homology and fractal dimension; our results are the first rigorous analogue of those comparisons. Spe
From playlist AATRN 2018

Homotopy Group - (1)Dan Licata, (2)Guillaume Brunerie, (3)Peter Lumsdaine
(1)Carnegie Mellon Univ.; Member, School of Math, (2)School of Math., IAS, (3)Dalhousie Univ.; Member, School of Math April 11, 2013 In this general survey talk, we will describe an approach to doing homotopy theory within Univalent Foundations. Whereas classical homotopy theory may be des
From playlist Mathematics

Emilie Purvine (5/2/21): Homology of Graphs and Hypergraphs
Graphs and hypergraphs are typically studied from a combinatorial perspective. A graph being a collection of vertices and pairwise relationships (edges) among the vertices, and a hypergraph capturing multi-way or groupwise relationships (hyperedges) among the vertices. But both of these ob
From playlist TDA: Tutte Institute & Western University - 2021

Algebraic Topology - 11.3 - Homotopy Equivalence
We sketch why that the homotopy category is a category.
From playlist Algebraic Topology

An interesting homotopy (in fact, an ambient isotopy) of two surfaces.
From playlist Algebraic Topology
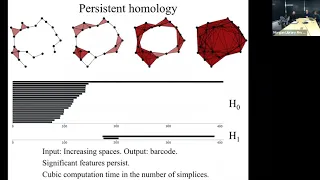
An introduction to persistent homology
Title: An introduction to persistent homology Venue: Webinar for DELTA (Descriptors of Energy Landscape by Topological Analysis Abstract: This talk is an introduction to applied and computational topology, in particular as related to the study of energy landscapes arising in chemistry. W
From playlist Tutorials

Omer Bobrowski: Random Simplicial Complexes, Lecture I
A simplicial complex is a collection of vertices, edges, triangles, tetrahedra and higher dimensional simplexes glued together. In other words, it is a higher-dimensional generalization of a graph. In recent years there has been a growing effort in developing the theory of random simplicia
From playlist Workshop: High dimensional spatial random systems

Homology cobordism and triangulations – Ciprian Manolescu – ICM2018
Geometry | Topology Invited Lecture 5.5 | 6.1 Homology cobordism and triangulations Ciprian Manolescu Abstract: The study of triangulations on manifolds is closely related to understanding the three-dimensional homology cobordism group. We review here what is known about this group, with
From playlist Geometry

Intuitive Persistence - Damiano - 2020
Intuitive Persistence This lecture introduces the persistent homology of a filtration of a simplicial complex. In each dimension inclusions of the filtration subcomplexes induce a sequence of maps on the homology vector spaces of the given dimension of the subcomplexes. Tracking cycles fr
From playlist Applied Topology - David Damiano - 2020

Anthony Henderson: Hilbert Schemes Lecture 9
SMRI Seminar Series: 'Hilbert Schemes' Lecture 9 Correspondences in homology Anthony Henderson (University of Sydney) This series of lectures aims to present parts of Nakajima’s book `Lectures on Hilbert schemes of points on surfaces’ in a way that is accessible to PhD students intereste
From playlist SMRI Course: Hilbert Schemes

Jose Perea (5/2/21): Quasiperiodicity and Persistent Kunneth Theorems
A signal is said to be quasiperiodic if its constitutive frequencies are linearly independent over the rationals. With appropriate parameters, the sliding window embedding of such a function can be shown to be dense in a torus of dimension equal to the number of independent frenquencies. I
From playlist TDA: Tutte Institute & Western University - 2021

Hannah Alpert (4/15/22): Homology of sliding-squares configuration spaces
The configuration space of n ordered points in the plane is homotopy equivalent to that of n ordered unit squares sliding in the plane. How does the rank of its degree-j homology group change if the squares are confined to the p by q rectangle? This rank turns out to be much bigger, grow
From playlist Vietoris-Rips Seminar

Contact non-squeezing via selective symplectic homology - Igor Uljarević
Joint IAS/Princeton/Montreal/Paris/Tel-Aviv Symplectic Geometry Zoominar Topic: Contact non-squeezing via selective symplectic homology Speaker: Igor Uljarević Affiliation: University of Belgrade Date: October 14, 2022 I will introduce a new version of symplectic homology that resembles
From playlist Mathematics
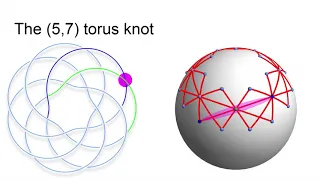
Knots, three-manifolds and instantons – Peter Kronheimer & Tomasz Mrowka – ICM2018
Plenary Lecture 11 Knots, three-manifolds and instantons Peter Kronheimer & Tomasz Mrowka Abstract: Over the past four decades, input from geometry and analysis has been central to progress in the field of low-dimensional topology. This talk will focus on one aspect of these developments
From playlist Plenary Lectures

An introduction to homology | Algebraic Topology | NJ Wildberger
We briefly describe the higher homotopy groups which extend the fundamental group to higher dimensions, trying to capture what it means for a space to have higher dimensional holes. Homology is a commutative theory which also deals with this issue, assigning to a space X a series of homolo
From playlist Algebraic Topology