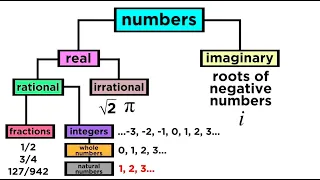
What are the Types of Numbers? Real vs. Imaginary, Rational vs. Irrational
We've mentioned in passing some different ways to classify numbers, like rational, irrational, real, imaginary, integers, fractions, and more. If this is confusing, then take a look at this handy-dandy guide to the taxonomy of numbers! It turns out we can use a hierarchical scheme just lik
From playlist Algebra 1 & 2

Introduction to the Cardinality of Sets and a Countability Proof
Introduction to Cardinality, Finite Sets, Infinite Sets, Countable Sets, and a Countability Proof - Definition of Cardinality. Two sets A, B have the same cardinality if there is a bijection between them. - Definition of finite and infinite sets. - Definition of a cardinal number. - Discu
From playlist Set Theory

As part of the college algebra series, this Center of Math video will teach you the basics of functions, including how they're written and what they do.
From playlist Basics: College Algebra

This video explains what a mathematical function is and how it defines a relationship between two sets, the domain and the range. It also introduces three important categories of function: injective, surjective and bijective.
From playlist Foundational Math

Formal Definition of a Function using the Cartesian Product
Learning Objectives: In this video we give a formal definition of a function, one of the most foundation concepts in mathematics. We build this definition out of set theory. **************************************************** YOUR TURN! Learning math requires more than just watching vid
From playlist Discrete Math (Full Course: Sets, Logic, Proofs, Probability, Graph Theory, etc)

Classification of Real Numbers, Inequalities, and Number Line
I define and discuss Real Numbers their subsets of Rational Numbers, Integers, Whole Numbers, Natural Numbers, and finally Irrational Numbers. I finish with Inequalities and the Number line at 23:53 Find free review test, useful notes and more at http://www.mathplane.com If you'd like to
From playlist Algebra 1

Logic: The Structure of Reason
As a tool for characterizing rational thought, logic cuts across many philosophical disciplines and lies at the core of mathematics and computer science. Drawing on Aristotle’s Organon, Russell’s Principia Mathematica, and other central works, this program tracks the evolution of logic, be
From playlist Logic & Philosophy of Mathematics

Jean-Bernard Lasserre: The moment-LP and moment-SOS approaches
Find this video and other talks given by worldwide mathematicians on CIRM's Audiovisual Mathematics Library: http://library.cirm-math.fr. And discover all its functionalities: - Chapter markers and keywords to watch the parts of your choice in the video - Videos enriched with abstracts, b
From playlist Control Theory and Optimization

Non-commutative polynomial optimisation problems (...) - A. Acín - Workshop 2 - CEB T3 2017
Antonio Acín / 25.10.17 Non-commutative polynomial optimisation problems in quantum information theory We discuss questions in quantum physics that can be cast as non-commutative polynomial optimisation problems and discuss their solution in terms of semi-definite programming. This range
From playlist 2017 - T3 - Analysis in Quantum Information Theory - CEB Trimester

Number theory Full Course [A to Z]
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure #mathematics devoted primarily to the study of the integers and integer-valued functions. Number theorists study prime numbers as well as the properties of objects made out of integers (for example, ratio
From playlist Number Theory

Cyril Cohen - Hierarchy Builder
Libraries of machine checked code are, nowadays, organized around hierarchies of algebraic structures. Unfortunately the language of Type Theory and the features provided by modern proof assistants make the construction of a hierarchy hard even for expert users. The difficulty begins with
From playlist Workshop Schlumberger 2022 : types dépendants et formalisation des mathématiques

Anders Hansen: What is the Solvability Complexity Index SCI....
Anders Hansen: What is the Solvability Complexity Index (SCI) of your problem? - On the SCI Hierarchy and the foundations of computational mathematics Abstract: This talk addresses some of the fundamental barriers in the theory of computations. Many computational problems can be solved as
From playlist HIM Lectures: Trimester Program "Mathematics of Signal Processing"

The successor-limit hierarchy and ordinals II | Data structures Math Foundations 183
This video is a continuation of MF181, in which we reviewed and extended the successor-limit hierarchy of very big arithmetical operations. In this video we want to compare this hierarchy with ordinal numbers in modern set theory. Sadly, modern set theory is a theory without a proper fou
From playlist Math Foundations

Joel David Hamkins : The hierarchy of second-order set theories between GBC and KM and beyond
Abstract: Recent work has clarified how various natural second-order set-theoretic principles, such as those concerned with class forcing or with proper class games, fit into a new robust hierarchy of second-order set theories between Gödel-Bernays GBC set theory and Kelley-Morse KM set th
From playlist Logic and Foundations

Hierarchical Modeling of High-dimensional Human Immuno-phenotypic Diversity by Saumyadipta Pyne
DISCUSSION MEETING : MATHEMATICAL AND STATISTICAL EXPLORATIONS IN DISEASE MODELLING AND PUBLIC HEALTH ORGANIZERS : Nagasuma Chandra, Martin Lopez-Garcia, Carmen Molina-Paris and Saumyadipta Pyne DATE & TIME : 01 July 2019 to 11 July 2019 VENUE : Madhava Lecture Hall, ICTS, Bangalore
From playlist Mathematical and statistical explorations in disease modelling and public health

IMS Public Lecture: Foundations of Mathematics: An Optimistic Message
Stephen G. Simpson, Pennsylvania State University, USA
From playlist Public Lectures

Wolfram Physics Project: Axiomatization of the Computational Universe Tuesday, Feb. 16, 2021
This is a Wolfram Physics Project working session about the axiomatization of the Computational Universe. Begins at 1:36 Originally livestreamed at: https://twitch.tv/stephen_wolfram Stay up-to-date on this project by visiting our website: http://wolfr.am/physics Check out the announceme
From playlist Wolfram Physics Project Livestream Archive
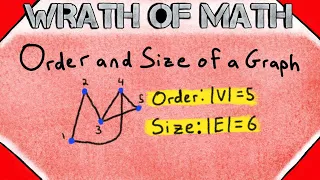
Order and Size of a Graph | Graph Theory
What is the order and size of a graph? We'll go over them both in this math lesson! A graph is an ordered pair with a vertex set and an edge set. The order of a graph is the cardinality of its vertex set, which is the number of vertices in the graph. The size of a graph is the cardinality
From playlist Graph Theory

A Hierarchy of Infinities | Infinite Series | PBS Digital Studios
Viewers like you help make PBS (Thank you 😃) . Support your local PBS Member Station here: https://to.pbs.org/donateinfi There are different sizes of infinity. It turns out that some are larger than others. Mathematician Kelsey Houston-Edwards breaks down what these different sizes are an
From playlist An Infinite Playlist
