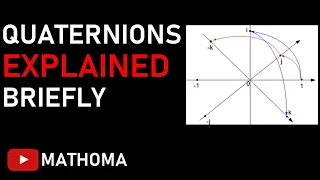
This is a video I have been wanting to make for some time, in which I discuss what the quaternions are, as mathematical objects, and how we do calculations with them. In particular, we will see how the fundamental equation of the quaternions i^2=j^2=k^2=ijk=-1 easily generates the rule for
From playlist Quaternions

What is the difference of a trapezoid and an isosceles trapezoid
👉 Learn how to solve problems with trapezoids. A trapezoid is a four-sided shape (quadrilateral) such that one pair of opposite sides are parallel. Some of the properties of trapezoids are: one pair of opposite sides are parallel, etc. A trapezoid is isosceles is one pair of opposite sides
From playlist Properties of Trapezoids

👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships
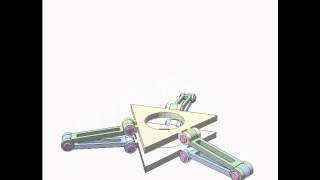
An embodiment of "Sarrus linkage 1". Two planes of two planar slider-crank mechanisms are not necessary to be perpendicular to each other. It is enough that they are not parallel.
From playlist Mechanisms

This is the other case. The first one was rotation about yb and xa, or if you like x into a and y into b, this one is rotation about xb and ya or x into b and y into a. Now I have a strange feeling that there are again an inifinite number of mixed cases, but I will not think about that now
From playlist Fractal

What are some characteristics of an isosceles trapezoid
👉 Learn how to solve problems with trapezoids. A trapezoid is a four-sided shape (quadrilateral) such that one pair of opposite sides are parallel. Some of the properties of trapezoids are: one pair of opposite sides are parallel, etc. A trapezoid is isosceles is one pair of opposite sides
From playlist Properties of Trapezoids

Using the pythagorean theorem to a rhombus
👉 Learn how to solve problems with rhombuses. A rhombus is a parallelogram such that all the sides are equal. Some of the properties of rhombuses are: all the sides are equal, each pair of opposite sides are parallel, each pair of opposite angles are equal, the diagonals bisect each other,
From playlist Properties of Rhombuses

Landau-Ginzburg - Seminar 5 - From quadratic forms to bicategories
This seminar series is about the bicategory of Landau-Ginzburg models LG, hypersurface singularities and matrix factorisations. In this seminar Dan Murfet starts with quadratic forms and introduces Clifford algebras, their modules and bimodules and explains how these fit into a bicategory
From playlist Metauni

Max Jensen: Convergent semi-Lagrangian methods for the Monge-Ampère equation on unstructured grids
The lecture was held within the framework of the Hausdorff Trimester Program Multiscale Problems: Workshop on Numerical Inverse and Stochastic Homogenization. (15.02.2017) In this presentation I will discuss a semi-Lagrangian discretisation of the Monge-Ampère operator on P1 finite elemen
From playlist HIM Lectures: Trimester Program "Multiscale Problems"

What are the properties that make up a rhombus
👉 Learn how to solve problems with rhombuses. A rhombus is a parallelogram such that all the sides are equal. Some of the properties of rhombuses are: all the sides are equal, each pair of opposite sides are parallel, each pair of opposite angles are equal, the diagonals bisect each other,
From playlist Properties of Rhombuses

V. Tosatti - $C^{1,1}$ estimates for complex Monge-Ampère equations
I will discuss a method that we recently introduced in collaboration with Chu and Weinkove which gives interior C1,1 estimates for the non-degenerate complex Monge-Ampère equation on compact Kähler manifolds (possibly with boundary). The method is sufficiently robust to also give C1,1 regu
From playlist Complex analytic and differential geometry - a conference in honor of Jean-Pierre Demailly - 6-9 juin 2017
Strongly log concave polynomials...Bases of Matroids - Shayan Oveis Gharan
More videos on http://video.ias.edu
From playlist Mathematics

Worldwide Calculus: Local Extrema
Lecture on 'Local Extrema' from 'Worldwide Multivariable Calculus'. For more lecture videos and $10 digital textbooks, visit www.centerofmath.org.
From playlist Multivariable Derivatives

Complex Stochastic Models and their Applications by Subhroshekhar Ghosh
PROGRAM: TOPICS IN HIGH DIMENSIONAL PROBABILITY ORGANIZERS: Anirban Basak (ICTS-TIFR, India) and Riddhipratim Basu (ICTS-TIFR, India) DATE & TIME: 02 January 2023 to 13 January 2023 VENUE: Ramanujan Lecture Hall This program will focus on several interconnected themes in modern probab
From playlist TOPICS IN HIGH DIMENSIONAL PROBABILITY

Singular Learning Theory - Seminar 27 - Jet schemes II
This seminar series is an introduction to Watanabe's Singular Learning Theory, a theory about algebraic geometry and statistical learning theory. This week Dan gives the second in a series of talks about jet schemes and arc schemes, an alternative point of view on the information present i
From playlist Singular Learning Theory

F. Boarotto - Normal forms around regular abnormal curves in rank-two distributions (Part 1)
Let (M, ∆) be a rank-two sub-Riemannian structure on a smooth manifold M, and let x, y be any two points on M. In this talk I will present some recent results concerning the description of the set Ω(y), of all the horizontal curves joining x and y, in the vicinity of a rank-two-nice singul
From playlist Journées Sous-Riemanniennes 2018

23. Generalized Linear Models (cont.)
MIT 18.650 Statistics for Applications, Fall 2016 View the complete course: http://ocw.mit.edu/18-650F16 Instructor: Philippe Rigollet In this lecture, Prof. Rigollet talked about strict concavity, optimization methods, quadratic approximation, Newton-Raphson method, and Fisher-scoring me
From playlist MIT 18.650 Statistics for Applications, Fall 2016

In this video, I show a very neat result about dual spaces: Namely, any basis of V* is automatically a dual basis of some basis of V. Even though this result is very interesting, it's the proof that makes this very exciting, by simply using the fact that V and V** are 'very' isomorphic. En
From playlist Dual Spaces
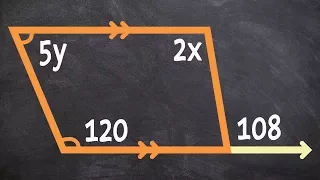
Finding the value of x using a trapezoid alternate interior angles and supplementary
👉 Learn how to solve problems with trapezoids. A trapezoid is a four-sided shape (quadrilateral) such that one pair of opposite sides are parallel. Some of the properties of trapezoids are: one pair of opposite sides are parallel, etc. A trapezoid is isosceles is one pair of opposite sides
From playlist Properties of Trapezoids

Félix Otto: The matching problem
The optimal transport between a random atomic measure described by the Poisson point process and the Lebesgue measure in d-dimensional space has received attention in diverse communities. Heuristics suggest that on large scales, the displacement potential, which is a solution of the highly
From playlist Probability and Statistics