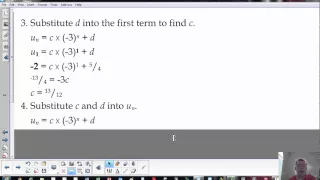
Evaluating Recurrence Relations (1 of 4: When do you apply Recurrence Relations?)
More resources available at www.misterwootube.com
From playlist Further Integration

👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

Richard Taylor "Reciprocity Laws" [2012]
Slides for this talk: https://drive.google.com/file/d/1cIDu5G8CTaEctU5qAKTYlEOIHztL1uzB/view?usp=sharing Richard Taylor "Reciprocity Laws" Abstract: Reciprocity laws provide a rule to count the number of solutions to a fixed polynomial equation, or system of polynomial equations, modu
From playlist Number Theory

👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

What is an angle and it's parts
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships

Using the properties of rectangles to solve for x
👉 Learn how to solve problems with rectangles. A rectangle is a parallelogram with each of the angles a right angle. Some of the properties of rectangles are: each pair of opposite sides are equal, each pair of opposite sides are parallel, all the angles are right angles, the diagonals are
From playlist Properties of Rectangles

Smooth Transition Function in One Dimension | Smooth Transition Function Part 1
#SoME2 This video gives a detailed construction of transition function for various levels of smoothness. Sketch of proofs for 4 theorems regarding smoothness: https://kaba.hilvi.org/homepage/blog/differentiable.htm Faà di Bruno's formula: https://en.wikipedia.org/wiki/Fa%C3%A0_di_Bruno%2
From playlist Summer of Math Exposition 2 videos
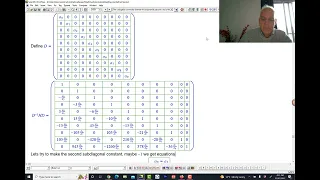
Advice Maths| The conjugation connection between the exp polyseries and Hermite on-maxels | Wild Egg
In studying Harriot Pascal maxels in Algebraic Calculus One, we realized that a suitable conjugation simplifies their study significantly, and sheds light on the close connection between the exponential on-series and the Binomial theorem and associated coefficients. Using the same reasonin
From playlist Maxel inverses and orthogonal polynomials (non-Members)

Discrete Math - 8.1.1 Modeling with Recurrence Relations
Modeling some of the famous combinatoric questions (Tower of Hanoi, Fibonacci) with recurrence relations. Textbook: Rosen, Discrete Mathematics and Its Applications, 7e Playlist: https://www.youtube.com/playlist?list=PLl-gb0E4MII28GykmtuBXNUNoej-vY5Rz
From playlist Discrete Math I (Entire Course)

CCSS What is an angle bisector
👉 Learn how to define angle relationships. Knowledge of the relationships between angles can help in determining the value of a given angle. The various angle relationships include: vertical angles, adjacent angles, complementary angles, supplementary angles, linear pairs, etc. Vertical a
From playlist Angle Relationships
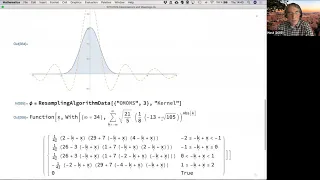
Interpolations and Mappings with Applications in Image Processing
In this talk, Markus van Almsick reviews the most popular and most advanced interpolation methods and discusses their merits and shortcomings. The Wolfram Language provides many interpolation methods to construct continuous functions from discrete data points. Furthermore, interpolations a
From playlist Wolfram Technology Conference 2020

Some inter-relations between random matrix ensembles - Peter Forrester
Peter Forrester University of Melbourne October 16, 2013 In the early 1960's Dyson and Mehta found that the CSE relates to the COE. I'll discuss generalizations as well as other settings in random matrix theory in which β relates to 4/β. For more videos, visit http://video.ias.edu
From playlist Mathematics

The PROOF: e and pi are transcendental
Today’s video is dedicated to introducing you to two of the holy grails of mathematics, proofs that e and pi are transcendental numbers. For the longest time I was convinced that these proofs were simply out of reach of a self-contained episode of Mathologer, and I even said so in a video
From playlist Recent videos

These Feisty Hermit Crabs Brawl Over Snail Shells | Deep Look
Hermit crabs are *obsessed* with snail shells. These crafty little crabs, found in California's rocky intertidal zone, are more than happy to let the snails build them a perfect home. When the crabs find a snail shell they like, they hop right into their new abode. SUBSCRIBE to Deep Look!
From playlist Deep Look | Series | KQED

Advice for Amateur Mathematicians | The joy of maxel number theory and Hermite polyns |Wild Egg Math
We extend our two dimensional number theory point of view to the case of Hermite polynomials. These actually come in two different kinds: called the probabilists' and the physicists' versions. Can we find some interesting patterns when we express these in a two-dimensional setting as a tr
From playlist Maxel inverses and orthogonal polynomials (non-Members)

Under the Sea - With Helen Scales
A dive into the spiralling world of seashells and the bizarre animals that make them. Helen Scales explains how hermit crabs like to party and butterflies learnt to swim. Watch the Q&A: https://www.youtube.com/watch?v=GqBHjBDgLfY Subscribe for regular science videos: http://bit.ly/RiSubsc
From playlist Ri Talks

Series solution of the Hermite differential equation. Shows how to construct the Hermite polynomials. Join me on Coursera: Differential equations for engineers https://www.coursera.org/learn/differential-equations-engineers Matrix algebra for engineers https://www.coursera.org/learn/matr
From playlist Differential Equations with YouTube Examples

Long-term history and ephemeral configurations – Catherine Goldstein – ICM2018
Plenary Lecture 12 Long-term history and ephemeral configurations Catherine Goldstein Abstract: Mathematical concepts and results have often been given a long history, stretching far back in time. Yet recent work in the history of mathematics has tended to focus on local topics, over a s
From playlist Plenary Lectures

The idea of ‘atonement’ sounds very old-fashioned and is deeply rooted in religious tradition. To atone means, in essence, to acknowledge one’s capacity for wrongness and one’s readiness for apology and desire for change. It’s a concept that every society needs at its center. For gifts and
From playlist RELATIONSHIPS