
Graham Leigh: On the computational content of classical sequent calculus
The lecture was held within the framework of the Hausdorff Trimester Program: Types, Sets and Constructions. Abstract: Computational interpretations of classical logic are entwined with constructive proofs of Herbrand's Theorem which states, its simplest form, that for every valid existen
From playlist Workshop: "Proofs and Computation"

Michael Temkin - Wild coverings of Berkovich curves
I will describe the structure of finite morphisms between smooth Berkovich curves. The tame case is well known so the accent will be on the wild case. In particular, I will describe the loci of points of multiplicity n and their relation to Herbrand function and the ramification theory. If
From playlist A conference in honor of Arthur Ogus on the occasion of his 70th birthday

Artur Avila "Poincaré series and renormalization"
Originaire du Brésil, Artur Avila obtient son doctorat en 2001 à l'IMPA. En 2008 il reçoit le prix de l'EMS puis le Grand Prix Jacques Herbrand de l'Académie des sciences en 2009. Il a été conférencier plénier au Congrès international des mathématiciens en 2010. Il est Directeur de Recherc
From playlist Colloque Scientifique International Poincaré 100
Nalini Anantharaman "From the three-body problem to quantum mechanics"
Résumé Poincaré annonçait, dans l'introduction des Méthodes nouvelles de la mécanique céleste, fournit « un terrain solide sur lequel on pourra s'appuyer avec confiance ». C'est avec cette confiance que les physiciens du début du 20ème siècle se sont attaqués à l'étude de l'atome d'hélium,
From playlist Colloque Scientifique International Poincaré 100

What are the properties that make up a rhombus
👉 Learn how to solve problems with rhombuses. A rhombus is a parallelogram such that all the sides are equal. Some of the properties of rhombuses are: all the sides are equal, each pair of opposite sides are parallel, each pair of opposite angles are equal, the diagonals bisect each other,
From playlist Properties of Rhombuses

Potential Automorphy - Richard Taylor
Richard Taylor Institute for Advanced Study October 4, 2010 I will introduce l-adic representations and what it means for them to be automorphic, talk about potential automorphy as an alternative to automorphy, explain what can currently be proved (but not how) and discuss what seem to me
From playlist Mathematics

Hugo Duminil Copin - Compter les chemins auto-évitants sur le réseau en nid d'abeille
IHES, Prix Jacques Herbrand 2017 Réalisation technique : Antoine Orlandi (GRICAD) | Tous droits réservés
From playlist Des mathématiciens primés par l'Académie des Sciences 2017

What are the properties that make up a parallelogram
👉 Learn how to solve problems with parallelograms. A parallelogram is a four-sided shape (quadrilateral) such that each pair of opposite sides are parallel and are equal. Some of the properties of parallelograms are: each pair of opposite sides are equal, each pair of opposite sides are pa
From playlist Properties of Parallelograms

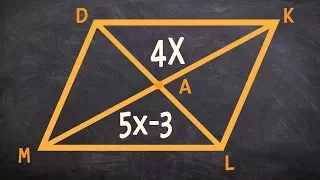
Using the properties of parallelograms to solve for the missing diagonals
👉 Learn how to solve problems with parallelograms. A parallelogram is a four-sided shape (quadrilateral) such that each pair of opposite sides are parallel and are equal. Some of the properties of parallelograms are: each pair of opposite sides are equal, each pair of opposite sides are pa
From playlist Properties of Parallelograms

What is the difference of a trapezoid and an isosceles trapezoid
👉 Learn how to solve problems with trapezoids. A trapezoid is a four-sided shape (quadrilateral) such that one pair of opposite sides are parallel. Some of the properties of trapezoids are: one pair of opposite sides are parallel, etc. A trapezoid is isosceles is one pair of opposite sides
From playlist Properties of Trapezoids

Using the pythagorean theorem to a rhombus
👉 Learn how to solve problems with rhombuses. A rhombus is a parallelogram such that all the sides are equal. Some of the properties of rhombuses are: all the sides are equal, each pair of opposite sides are parallel, each pair of opposite angles are equal, the diagonals bisect each other,
From playlist Properties of Rhombuses
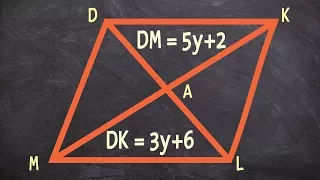
Applying the properties of a rhombus to determine the length of a diagonal
👉 Learn how to solve problems with rhombuses. A rhombus is a parallelogram such that all the sides are equal. Some of the properties of rhombuses are: all the sides are equal, each pair of opposite sides are parallel, each pair of opposite angles are equal, the diagonals bisect each other,
From playlist Properties of Rhombuses

What are some characteristics of an isosceles trapezoid
👉 Learn how to solve problems with trapezoids. A trapezoid is a four-sided shape (quadrilateral) such that one pair of opposite sides are parallel. Some of the properties of trapezoids are: one pair of opposite sides are parallel, etc. A trapezoid is isosceles is one pair of opposite sides
From playlist Properties of Trapezoids
Using the properties of a rhombus to determine the side of a rhombus
👉 Learn how to solve problems with rhombuses. A rhombus is a parallelogram such that all the sides are equal. Some of the properties of rhombuses are: all the sides are equal, each pair of opposite sides are parallel, each pair of opposite angles are equal, the diagonals bisect each other,
From playlist Properties of Rhombuses

Ivo Hofacker: RNA secondary structures
Recording during the meeting "AlgoSB 2019 - Mathematical and Computational Methods for Structured RiboNucleic Acids" the January 14, 2019 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by w
From playlist Mathematics in Science & Technology
From playlist Pre-Algebra/Introductory Algebra

What Is Data Structure? | Introduction To Data Structures | Data Structures Tutorial | Simplilearn
🔥Post Graduate Program In Full Stack Web Development: https://www.simplilearn.com/pgp-full-stack-web-development-certification-training-course?utm_campaign=WhatIsDataStructures-CCxgUXrbFWY&utm_medium=DescriptionFF&utm_source=youtube 🔥Caltech Coding Bootcamp (US Only): https://www.simplilea
From playlist Data Structures & Algorithms [2022 Updated]

Isomorphic Structures of any Kind are `Equal' in HoTT: But What... Structure? - Peter Aczel
Peter Aczel The Unviersity of Manchester; Member,School of Mathematics February 7, 2013 For more videos, visit http://video.ias.edu
From playlist Mathematics

Structures in C Programming | Introduction to Structures in C | C Language Tutorial | Simplilearn
This video by Simplilearn will explain to you about Structures in C Programming. Introduction to Structures in C Language Tutorial will explain you what are structures in C, C structures example programs, discuss on structure within structure, structure declaration and initialization. The
From playlist C++ Tutorial Videos

Geometry - Ch. 1: Basic Concepts (26 of 49) Congruent Sides and Congruent Angles: Ex.
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain how to identify quadrilaterals, triangles that are equilateral triangles, quadrilaterals that are also a square by by observing the angles, sides, and their congruences of the figures. Next v
From playlist GEOMETRY CH 1 BASIC CONCEPTS