
Analytic continuation in higher dimensions
In this short lecture I will prove the Hartogs theorem stating that holomorphic functions can be continued across compacts subsets if the dimension is at least 2. The proof will use solution of the del bar problem with compact support. For more details see Section 2.3 in Hormander's "Intro
From playlist Several Complex Variables

A Complete Dichotomy Rises from the Capture of Vanishing Signatures - Jin-Yi Cai
Jin-Yi Cai University of Wisconsin November 19, 2012 Holant Problems are a broad framework to describe counting problems. The framework generalizes counting Constraint Satisfaction Problems and partition functions of Graph Homomorphisms. We prove a complexity dichotomy theorem for Holant
From playlist Mathematics

The Monge - Ampère equations, the Bergman kernel... (Lecture 1)by Kengo Hirachi
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019

John McCarthy: Norm-preserving extensions of bounded holomorphic functions
Recording during the meeting "Interpolation in Spaces of Analytic Functions" the November 18, 2019 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audio
From playlist Analysis and its Applications

Olivia Dumitrescu - Lagrangian Fibration of the de Rham Moduli Space and Gaiotto Correspondence
There have been new developments in understanding Lagrangian fibrations of the de Rham moduli space in connection to Lagrangian stratifications of the Dolbeault moduli space through biholomorphic isomorphisms of the Lagrangian fibers. I will report recent results by different groups of aut
From playlist Resurgence in Mathematics and Physics

A Combinatorial Proof of the Chernoff-Hoeffding Bound...- Valentine Kabanets
Valentine Kabanets Simon Fraser University; Institute for Advanced Study March 30, 2010 We give a simple combinatorial proof of the Chernoff-Hoeffding concentration bound for sums of independent Boolean random variables. Unlike the standard proofs, our proof does not rely on the method of
From playlist Mathematics

Lectures on compactness in the ̄∂–Neumann problem (Lecture 4) by Emil Straube
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019

Set Theory (Part 2): ZFC Axioms
Please feel free to leave comments/questions on the video and practice problems below! In this video, I introduce some common axioms in set theory using the Zermelo-Fraenkel w/ choice (ZFC) system. Five out of nine ZFC axioms are covered and the remaining four will be introduced in their
From playlist Set Theory by Mathoma
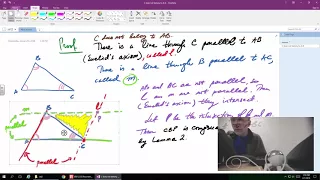
A theorem about isosceles -- Proofs
This lecture is on Introduction to Higher Mathematics (Proofs). For more see http://calculus123.com.
From playlist Proofs

SEPARATION BUT MATHEMATICALLY: What Types of Mathematical Topologies are there? | Nathan Dalaklis
The title of this video is a bit convoluted. What do you mean by "Separation but Mathematically"? Well, in this video I'll be giving a (very diluted) answer to the question "What types of mathematical topologies are there?" by introducing the separation axioms in topology. The separation
From playlist The New CHALKboard

Applications of the theory of the ̄∂ equation (Lecture 2) by Vamsi Pingali
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019

On local interdefinability of analytic functions - T. Servi - Workshop 3 - CEB T1 2018
Tamara Servi (Université Paris-Diderot) / 27.03.2018 On local interdefinability of (real and complex) analytic functions Given two (real or complex) analytic functions f and g, it is not sensible in general to ask whether they are first-order interdefinable as total functions (think of t
From playlist 2018 - T1 - Model Theory, Combinatorics and Valued fields

H. Reis - Introduction to holomorphic foliations (Part 4)
The purpose of this course is to present the basics of the general theory of (singular) holomorphic foliations. We will begin with the general definition of a (regular) foliation and its relation with Frobenius Theorem. We will then introduce the singular analogues of these notions in the
From playlist Ecole d'été 2019 - Foliations and algebraic geometry

Thomas Ransford: Constructive polynomial approximation in Banach spaces of holomorphic functions
Recording during the meeting "Interpolation in Spaces of Analytic Functions" the November 21, 2019 at the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM's Audio
From playlist Analysis and its Applications

Brill-Noether part 4: Noether's Theorem
From playlist Brill-Noether

An introduction to the Gromov-Hausdorff distance
Title: An introduction to the Gromov-Hausdorff distance Abstract: We give a brief introduction to the Hausdorff and Gromov-Hausdorff distances between metric spaces. The Hausdorff distance is defined on two subsets of a common metric space. The Gromov-Hausdorff distance is defined on any
From playlist Tutorials

Transversality and super-rigidity in Gromov-Witten Theory (Lecture – 02) by Chris Wendl
J-Holomorphic Curves and Gromov-Witten Invariants DATE:25 December 2017 to 04 January 2018 VENUE:Madhava Lecture Hall, ICTS, Bangalore Holomorphic curves are a central object of study in complex algebraic geometry. Such curves are meaningful even when the target has an almost complex stru
From playlist J-Holomorphic Curves and Gromov-Witten Invariants

In this lecture I prove the Cartan-Thullen theorem. For more information see my previous video on the channel.
From playlist Several Complex Variables

Background material on the Cauchy-Riemann equations (Lecture 1) by Debraj Chakrabarti
PROGRAM CAUCHY-RIEMANN EQUATIONS IN HIGHER DIMENSIONS ORGANIZERS: Sivaguru, Diganta Borah and Debraj Chakrabarti DATE: 15 July 2019 to 02 August 2019 VENUE: Ramanujan Lecture Hall, ICTS Bangalore Complex analysis is one of the central areas of modern mathematics, and deals with holomo
From playlist Cauchy-Riemann Equations in Higher Dimensions 2019
