
Introduction to Cylindrical Coordinates
Introduction to Cylindrical Coordinates Definition of a cylindrical coordinate and all of the formulas used to convert from cylindrical to rectangular and from rectangular to cylindrical. Examples are also given.
From playlist Calculus 3

Introduction to Cylindrical Coordinates
This video introduces cylindrical coordinates and shows how to convert between cylindrical coordinates and rectangular coordinates. http://mathispower4u.yolasite.com/
From playlist Quadric, Surfaces, Cylindrical Coordinates and Spherical Coordinates

C67 The physics of simple harmonic motion
See how the graphs of simple harmonic motion changes with changes in mass, the spring constant and the values correlating to the initial conditions (amplitude)
From playlist Differential Equations

Simple Harmonic Motion Example Question (1 of 3: Determining period of motion)
More resources available at www.misterwootube.com
From playlist Applications of Calculus to Mechanics

If the Laplacian of a function is zero everywhere, it is called Harmonic. Harmonic functions arise all the time in physics, capturing a certain notion of "stability", whenever one point in space is influenced by its neighbors.
From playlist Fourier

Introduction to Spherical Coordinates
This video defines spherical coordinates and explains how to convert between spherical and rectangular coordinates. http://mathispower4u.yolasite.com/
From playlist Quadric, Surfaces, Cylindrical Coordinates and Spherical Coordinates

Introduction to Simple Harmonic Motion
Please Subscribe here, thank you!!! https://goo.gl/JQ8Nys Introduction to Simple Harmonic Motion
From playlist Trigonometry
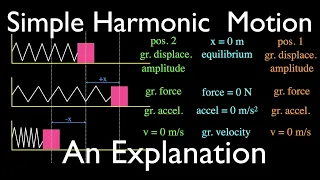
Simple Harmonic Motion (10 of 16): An Explanation
This video provides a step by step explanation of simple harmonic motion. You will learn the key terms that you needed to describe an oscillating mass as well as the important points in its motion where the displacement, force, acceleration and velocity will be the greatest and least. Sim
From playlist Simple Harmonic Motion, Waves and Vibrations

AWESOME Simple harmonic motion!
In this video show simple harmonic motion on spring and pendulums, used position sensor.
From playlist MECHANICS

Supersymmetry and Superspace, Part 3 - Jon Bagger
Supersymmetry and Superspace, Part 3 Jon Bagger Johns Hopkins University July 21, 2010
From playlist PiTP 2010

Daniel Stern - Level set methods for scalar curvature on three-manifolds
We'll discuss a circle of ideas developed over the last few years relating scalar curvature lower bounds to the structure of level sets of solutions to certain geometric pdes on 3-manifolds. We'll describe applications to the study of 3-manifold geometry and initial data sets in general re
From playlist Not Only Scalar Curvature Seminar

Out of Time Order correlators in systems interacting with a thermal bath by Soumyadeep Chaudhuri
Bangalore Area Strings Meeting - 2017 TIME : 31 July 2017 to 02 August 2017 VENUE:Madhava Lecture Hall, ICTS Bangalore Bengaluru now has a large group of string theorists, with 9 faculty members in the area, between ICTS and IISc. This is apart from a large group of postdocs and graduate
From playlist Bangalore Area Strings Meeting - 2017

Harmonic Maps between surfaces and Teichmuller theory (Lecture - 1) by Michael Wolf
Geometry, Groups and Dynamics (GGD) - 2017 DATE: 06 November 2017 to 24 November 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The program focuses on geometry, dynamical systems and group actions. Topics are chosen to cover the modern aspects of these areas in which research has b
From playlist Geometry, Groups and Dynamics (GGD) - 2017

[Lesson 9] QED Prerequisites - Mind Map of Angular Momentum Part I
This is the start of a high level review of the Quantum Theory of Angular Momentum. It is intended to point you into directions for deeper review. This material will lead us to our detailed review of non-relativistic scattering theory. Please consider supporting this channel on Patreon: h
From playlist QED- Prerequisite Topics

Higgs bundles, harmonic maps, and applications by Richard Wentworth
Higgs bundles URL: http://www.icts.res.in/program/hb2016 DATES: Monday 21 Mar, 2016 - Friday 01 Apr, 2016 VENUE : Madhava Lecture Hall, ICTS Bangalore DESCRIPTION: Higgs bundles arise as solutions to noncompact analog of the Yang-Mills equation. Hitchin showed that irreducible solutio
From playlist Higgs Bundles

Quadratic differentials and measured foliations on Riemann surfaces by Subhojoy Gupta
Program : Integrable? ?systems? ?in? ?Mathematics,? ?Condensed? ?Matter? ?and? ?Statistical? ?Physics ORGANIZERS : Alexander Abanov, Rukmini Dey, Fabian Essler, Manas Kulkarni, Joel Moore, Vishal Vasan and Paul Wiegmann DATE & TIME : 16 July 2018 to 10 August 2018 VENUE : Ramanujan L
From playlist Integrable systems in Mathematics, Condensed Matter and Statistical Physics

David Hilditch - Dual-Frame Generalized Harmonic Gauge on Hyperboloidal Slices - IPAM at UCLA
Recorded 28 October 2021. David Hilditch of the Instituto Superior Tecnico, University of Lisbon, presents "Dual-Frame Generalized Harmonic Gauge on Hyperboloidal Slices" at IPAM's Workshop II: Mathematical and Numerical Aspects of Gravitation. Abstract: Both for studies of cosmic censorsh
From playlist Workshop: Mathematical and Numerical Aspects of Gravitation

Harmonic Maps between surfaces and Teichmuller theory (Lecture - 2) by Michael Wolf
Geometry, Groups and Dynamics (GGD) - 2017 DATE: 06 November 2017 to 24 November 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The program focuses on geometry, dynamical systems and group actions. Topics are chosen to cover the modern aspects of these areas in which research has b
From playlist Geometry, Groups and Dynamics (GGD) - 2017
Harmonic maps into singular spaces - Brian Freidin
Variational Methods in Geometry Seminar Topic: Harmonic maps into singular spaces Speaker: Brian Freidin Affiliation: Brown University; Visitor, School of Mathematics Date: December 11, 2018 For more video please visit http://video.ias.edu
From playlist Variational Methods in Geometry
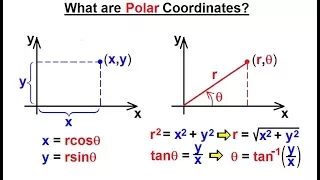
Calculus 2: Polar Coordinates (1 of 38) What are Polar Coordinates?
Visit http://ilectureonline.com for more math and science lectures! In this video I will explain what are polar coordinates and Cartesian coordinates. The Cartesian coordinates use x and y to locate a point on a plane, and the polar coordinates use r and theta to locate a point on a plane
From playlist THE "WHAT IS" PLAYLIST