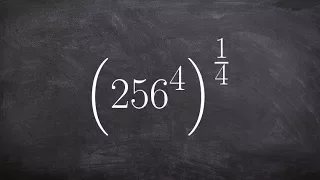
Applying the power rule to simplify an expression with a rational power
👉 Learn how to simplify rational powers using the power rule. There are some laws of exponents which might come handy when simplifying expressions with exponents. Some of the laws include the power rule which states that when an expression with an exponent is raised to another exponent tha
From playlist Raise an Exponent to a Fraction

Learn how to apply the power rule with fractional powers
👉 Learn how to simplify rational powers using the power rule. There are some laws of exponents which might come handy when simplifying expressions with exponents. Some of the laws include the power rule which states that when an expression with an exponent is raised to another exponent tha
From playlist Raise an Exponent to a Fraction

Simplifying an exponent using the power to power rule and rational powers
👉 Learn how to simplify rational powers using the power rule. There are some laws of exponents which might come handy when simplifying expressions with exponents. Some of the laws include the power rule which states that when an expression with an exponent is raised to another exponent tha
From playlist Raise an Exponent to a Fraction
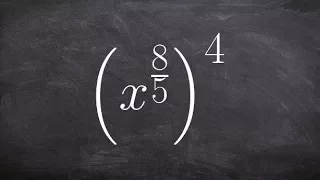
How to apply the power to power rule with rational exponents
👉 Learn how to simplify rational powers using the power rule. There are some laws of exponents which might come handy when simplifying expressions with exponents. Some of the laws include the power rule which states that when an expression with an exponent is raised to another exponent tha
From playlist Raise an Exponent to a Fraction
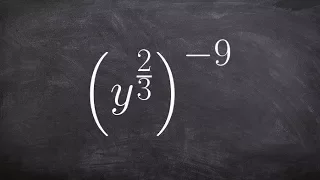
How to simplify a rational exponent raised to a negative power
👉 Learn how to simplify rational powers using the power rule. There are some laws of exponents which might come handy when simplifying expressions with exponents. Some of the laws include the power rule which states that when an expression with an exponent is raised to another exponent tha
From playlist Raise an Exponent to a Fraction

Apply the power rule with fractional exponents to simplify the expression
👉 Learn how to simplify rational powers using the power rule. There are some laws of exponents which might come handy when simplifying expressions with exponents. Some of the laws include the power rule which states that when an expression with an exponent is raised to another exponent tha
From playlist Raise an Exponent to a Fraction

Learn how to use the power rule with exponents with rational powers
👉 Learn how to simplify rational powers using the power rule. There are some laws of exponents which might come handy when simplifying expressions with exponents. Some of the laws include the power rule which states that when an expression with an exponent is raised to another exponent tha
From playlist Raise an Exponent to a Fraction

Simplifying an expression using the power rule of exponents
👉 Learn how to simplify rational powers using the power rule. There are some laws of exponents which might come handy when simplifying expressions with exponents. Some of the laws include the power rule which states that when an expression with an exponent is raised to another exponent tha
From playlist Raise an Exponent to a Fraction

Learn to evaluate an expression with a negative rational exponent ex 5, (cuberoot(8))^-1
👉 Learn how to simplify rational powers using the power rule. There are some laws of exponents which might come handy when simplifying expressions with exponents. Some of the laws include the power rule which states that when an expression with an exponent is raised to another exponent tha
From playlist Raise an Exponent to a Fraction

What are Bounded Sequences? | Real Analysis
What are bounded sequences? We go over the definition of bounded sequence in today's real analysis video lesson. We'll see examples of sequences that are bounded, and some that are bounded above or bounded below, but not both. We say a sequence is bounded if the set of values it takes on
From playlist Real Analysis

Bounds - Upper and Lower Bound Calculations | Grade 7-9 Maths Series | GCSE Maths Tutor
A video revising the techniques and strategies for looking at bounds calculations (Higher Only). This video is part of the Bounds module in GCSE maths, see my other videos below to continue with the series. These are the calculators that I recommend 💎 Casio fx-83GTX Scientific Calculat
From playlist GCSE Maths Videos

Math 101 Introduction to Analysis 091815: Least Upper Bound Axiom
The least upper bound axiom. Maximum and minimum of a set of real numbers. Upper bound; lower bound; bounded set. Least upper bound; greatest lower bound.
From playlist Course 6: Introduction to Analysis

Math 131 090516 Lecture #02 LUB property, Ordered Fields
Least Upper Bound Property and Greatest Lower Bound Property; Fields; Properties of Fields; Ordered Fields and properties; description of the real numbers (ordered field with LUB property containing rational numbers as subfield); Archimedean property #fields #orderedfields #leastupperboun
From playlist Course 7: (Rudin's) Principles of Mathematical Analysis
Real Analysis | The Supremum and Completeness of ℝ
We look at the notions of upper and lower bounds as well as least upper bounds and greatest lower bounds of sets of real numbers. We also prove an important classification lemma of least upper bounds. Finally, the completeness axiom of the real numbers is presented. Please Subscribe: ht
From playlist Real Analysis

Lecture 18 | Convex Optimization II (Stanford)
Lecture by Professor Stephen Boyd for Convex Optimization II (EE 364B) in the Stanford Electrical Engineering department. Professor Boyd's final lecture of the quarter is on Branch-and-bound methods. This course introduces topics such as subgradient, cutting-plane, and ellipsoid methods
From playlist Lecture Collection | Convex Optimization

When is a sequence bounded? - Week 1 - Lecture 12 - Sequences and Series
Subscribe at http://www.youtube.com/kisonecat
From playlist Ohio State: Calculus Two with Jim Fowler: Sequences and Series | CosmoLearning Mathematics

Real Analysis Chapter 1: The Axiom of Completeness
Welcome to the next part of my series on Real Analysis! Today we're covering the Axiom of Completeness, which is what opens the door for us to explore the wonderful world of the real number line, as it distinguishes the set of real numbers from that of the rational numbers. It allows us
From playlist Real Analysis

Using Bounds to Calculate Further Bounds
"Use lower and upper bounds within calculations to calculate a further lower/upper bound."
From playlist Number: Rounding & Estimation

Simplify monomials using law of exponents
👉 Learn how to simplify expressions using the power rule of exponents. When several terms of an expression is raised to an exponent outside the parenthesis, the exponent is distributed over the individual terms in the expression and the exponent outside the parenthesis is multiplied to eac
From playlist Simplify Using the Rules of Exponents
