
23 Algebraic system isomorphism
Isomorphic algebraic systems are systems in which there is a mapping from one to the other that is a one-to-one correspondence, with all relations and operations preserved in the correspondence.
From playlist Abstract algebra

Isometry groups of the projective line (I) | Rational Geometry Math Foundations 138 | NJ Wildberger
The projective line can be given a Euclidean structure, just as the affine line can, but it is a bit more complicated. The algebraic structure of this projective line supports some symmetries. Symmetry in mathematics is often most efficiently encoded with the idea of a group--a technical t
From playlist Math Foundations

Refraction (1 of 5) What is Refraction? An Explanation
Refraction, A conceptual qualitative explanation. Refraction is the change in direction of a ray of light as it passes from one medium to another. The amount of refraction is determined by the index of refraction of the media and the angle of incidence. For light, refraction follows Snell
From playlist Optics: Ray Diagrams, Reflection, Refraction, Thin Lens Equation

Atomistically inspired origami
Oxford Mathematics Public Lectures - Richard James - Atomistically inspired origami The World population is growing at about 80 million per year. As time goes by, there is necessarily less space per person. Perhaps this is why the scientific community seems to be obsessed with folding t
From playlist Oxford Mathematics Public Lectures

Grigori Avramidi: Topology of ends of finite volume, non positively curved manifolds
The lecture was held within the framework of the (Junior) Hausdorff Trimester Program Topology: "The Farrell-Jones conjecture" The structure of ends of nonpositively curved, locally symmetric manifolds is very well understood. In this talk, I will explain features of the locally symmetric
From playlist HIM Lectures: Junior Trimester Program "Topology"

Raytracing and raymarching simulations of non-euclidean geometries - Henry Segerman
Workshop on Topology: Identifying Order in Complex Systems Topic: Raytracing and raymarching simulations of non-euclidean geometries Speaker: Henry Segerman Affiliation: Oklahoma State University Date: December 4, 2020 For more video please visit http://video.ias.edu
From playlist Mathematics

Nicola Quercioli (1/13/21): Group equivariant non-expansive operators and their use in Deep Learning
Full Title: On the topological and geometrical properties of group equivariant non-expansive operators and their use in Deep Learning
From playlist ATMCS/AATRN 2020

How to determine the reference angle of an angle in degrees
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle

Find the reference angle of a negative angle
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle

Christina Sormani: A Course on Intrinsic Flat Convergence part 5
The lecture was held within the framework of the Hausdorff Trimester Program: Optimal Transportation and the Workshop: Winter School & Workshop: New developments in Optimal Transport, Geometry and Analysis
From playlist HIM Lectures 2015

Learn to find the reference angle of a negative angle in terms of pi
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle

Find the reference angle of a angle larger than 2pi
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle

Learn how to determine the reference angle of an angle in terms of pi
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle

Patrizio Frosini (8/30/21): On the role of group equivariant non-expansive operators in TDA
Group equivariant non-expansive operators (GENEOs) have been recently introduced as mathematical tools for approximating data observers, when data are represented by real-valued or vector-valued functions. The use of these operators is based on the assumption that the interpretation of dat
From playlist Beyond TDA - Persistent functions and its applications in data sciences, 2021

Lynne Walling: Understanding quadratic forms on lattices through generalised theta series
Abstract: Siegel introduced generalised theta series to study representation numbers of quadratic forms. Given an integral lattice L with quadratic form q, Siegel’s degree n theta series attached to L has a Fourier expansion supported on n-dimensional lattices, with Fourier coefficients th
From playlist Women at CIRM
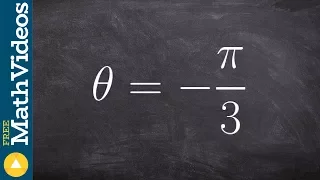
How to find the reference angle of a negative angle in terms of pi
👉 Learn how to find the reference angle of a given angle. The reference angle is the acute angle formed by the terminal side of an angle and the x-axis. To find the reference angle, we determine the quadrant on which the given angle lies and use the reference angle formula for the quadrant
From playlist Find the Reference Angle

Renato Bettiol - Scalar curvature rigidity and extremality in dimension 4
In this talk, I will discuss the Finsler--Thorpe trick for curvature operators in dimension 4, and how it can be combined with twisted spinor methods to show that large classes of compact 4-manifolds, with or without boundary, with nonnegative sectional curvature are area-extremal for scal
From playlist Not Only Scalar Curvature Seminar

What is color? What is it that determines the color of an object? And what the heck is refraction? Good thing we just learned about electromagnetic radiation! Especially the visible spectrum. Let's take a look. Watch the whole Classical Physics playlist: http://bit.ly/ProfDavePhysics1 Mo
From playlist Classical Physics

Geometry of the symmetric space SL(n,R)/SO(n,R) (Lecture - 3) by Pranab Sardar
Geometry, Groups and Dynamics (GGD) - 2017 DATE: 06 November 2017 to 24 November 2017 VENUE: Ramanujan Lecture Hall, ICTS, Bengaluru The program focuses on geometry, dynamical systems and group actions. Topics are chosen to cover the modern aspects of these areas in which research has b
From playlist Geometry, Groups and Dynamics (GGD) - 2017
