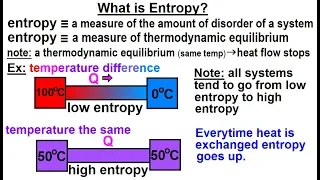
Physics - Thermodynamics 2: Ch 32.7 Thermo Potential (10 of 25) What is Entropy?
Visit http://ilectureonline.com for more math and science lectures! In this video explain and give examples of what is entropy. 1) entropy is a measure of the amount of disorder (randomness) of a system. 2) entropy is a measure of thermodynamic equilibrium. Low entropy implies heat flow t
From playlist PHYSICS 32.7 THERMODYNAMIC POTENTIALS

Graph Theory FAQs: 01. More General Graph Definition
In video 02: Definition of a Graph, we defined a (simple) graph as a set of vertices together with a set of edges where the edges are 2-subsets of the vertex set. Notice that this definition does not allow for multiple edges or loops. In general on this channel, we have been discussing o
From playlist Graph Theory FAQs
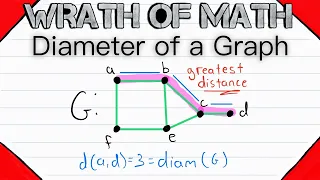
Diameter of a Graph | Graph Theory
What is the diameter of a graph in graph theory? This is a simple term we will define with examples in today's video graph theory lesson! Remember that the distance between two connected vertices in a graph is the length of a shortest path between those vertices. Here's my lesson on dist
From playlist Graph Theory
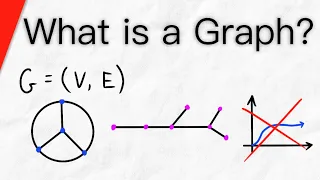
What is a Graph? | Graph Theory
What is a graph? A graph theory graph, in particular, is the subject of discussion today. In graph theory, a graph is an ordered pair consisting of a vertex set, then an edge set. Graphs are often represented as diagrams, with dots representing vertices, and lines representing edges. Each
From playlist Graph Theory

Graph Theory: 02. Definition of a Graph
In this video we formally define what a graph is in Graph Theory and explain the concept with an example. In this introductory video, no previous knowledge of Graph Theory will be assumed. --An introduction to Graph Theory by Dr. Sarada Herke. This video is a remake of the "02. Definitio
From playlist Graph Theory part-1

Simple Bounds on Vertex Connectivity | Graph Theory
We know that the vertex connectivity of a graph is the minimum number of vertices that can be deleted to disconnect it or make it trivial. We may then ask, what is an upper bound on the connectivity of a graph? What is a lower bound on the vertex connectivity of a graph? We give the most b
From playlist Graph Theory

The Definition of a Graph (Graph Theory)
The Definition of a Graph (Graph Theory) mathispower4u.com
From playlist Graph Theory (Discrete Math)
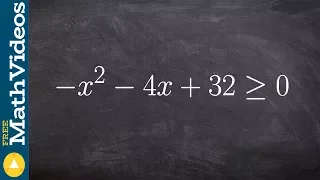
Solving a quadratic by graphing
Learn how to graph quadratic inequality. A quadratic inequality is an inequality is an inequality whose highest exponent on its variable is 2. The graph of a quadratic inequality is similar to the graph of a quadratic equation with the region inside or outside the parabola shaded. To grap
From playlist Graph Quadratic Inequality #Quadratics

What are Connected Graphs? | Graph Theory
What is a connected graph in graph theory? That is the subject of today's math lesson! A connected graph is a graph in which every pair of vertices is connected, which means there exists a path in the graph with those vertices as endpoints. We can think of it this way: if, by traveling acr
From playlist Graph Theory

Entropy-Based Bounds on Dimension Reduction in L_1 - Oded Regev
Oded Regev CNRS-ENS-Paris and Tel Aviv University November 28, 2011 For more videos, visit http://video.ias.edu
From playlist Mathematics

Topics in Combinatorics lecture 11.6 --- Two applications of Shearer's lemma
In the previous video I stated and proved Shearer's entropy lemma. Here I give two applications. The first provides an upper bound for the number of triangles a graph with m edges can have. The second is an upper bound for the size of a family of graphs with vertex set {1,2,...,n} if the i
From playlist Topics in Combinatorics (Cambridge Part III course)

Nexus Trimester - Mokshay Madiman (University of Delaware)
The Stam region, or the differential entropy region for sums of independent random vectors Mokshay Madiman (University of Delaware) February 25, 2016 Abstract: Define the Stam region as the subset of the positive orthant in [Math Processing Error] that arises from considering entropy powe
From playlist Nexus Trimester - 2016 - Fundamental Inequalities and Lower Bounds Theme
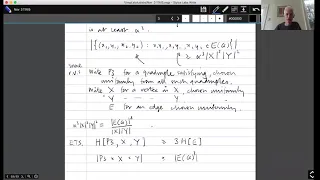
Topics in Combinatorics lecture 9.3 --- Using entropy to count paths of length 3
Having presented some (but by no means all) of the basic theory of entropy, I give an application to the following problem: let G be a bipartite graph of density c with vertex sets X and Y; prove that if x and x' are random vertices of X and y and y' are n vertices of Y, then the probabili
From playlist Topics in Combinatorics (Cambridge Part III course)

Some Half-Baked Thoughts about de Sitter Space - Leonard Susskind
High Energy Theory Seminar Topic: Some Half-Baked Thoughts about de Sitter Space Speaker: Leonard Susskind Affiliation: Stanford University Date: March 29, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

[BOURBAKI 2018] 20/10/2018 - 3/4 - Charles BORDENAVE
Charles BORDENAVE Normalité asymptotique des vecteurs propres de graphes d-réguliers aléatoires, d'après Ágnes Backhausz et Balázs Szegedy Soit P l’ensemble des matrices symétriques de taille n avec des entrées dans {0, 1}, nulles sur la diagonale et dont la somme de chaque ligne est éga
From playlist BOURBAKI - 2018

Breaking of Ensemble Equivalence in dense random graphs by Nicos Starreveld
Large deviation theory in statistical physics: Recent advances and future challenges DATE: 14 August 2017 to 13 October 2017 VENUE: Madhava Lecture Hall, ICTS, Bengaluru Large deviation theory made its way into statistical physics as a mathematical framework for studying equilibrium syst
From playlist Large deviation theory in statistical physics: Recent advances and future challenges

Breaking of ensemble equivalence in complex networks by Andrea Roccaverde
Large deviation theory in statistical physics: Recent advances and future challenges DATE: 14 August 2017 to 13 October 2017 VENUE: Madhava Lecture Hall, ICTS, Bengaluru Large deviation theory made its way into statistical physics as a mathematical framework for studying equilibrium syst
From playlist Large deviation theory in statistical physics: Recent advances and future challenges

Optimal Mixing of Glauber Dynamics: Entropy Factorization via High-Dimensional Expan - Zongchen Chen
Computer Science/Discrete Mathematics Seminar I Topic: Optimal Mixing of Glauber Dynamics: Entropy Factorization via High-Dimensional Expansion Speaker: Zongchen Chen Affiliation: Georgia Institute of Technology Date: February 22, 2021 For more video please visit http://video.ias.edu
From playlist Mathematics

A better description of entropy
I use this stirling engine to explain entropy. Entropy is normally described as a measure of disorder but I don't think that's helpful. Here's a better description. Visit my blog here: http://stevemould.com Follow me on twitter here: http://twitter.com/moulds Buy nerdy maths things here:
From playlist Best of
