
Functional Analysis Book for Beginners
This is a response to a question I received from a viewer. They want to learn functional analysis using the math book Introductory Functional Analysis with Applications by Kreyszig. They also want to know how long to study every day. Do you have any advice for learning functional analysis
From playlist Book Reviews

read this to learn functional analysis
read this to learn functional analysis Here is the book on amazon: https://amzn.to/2pMYOql (note this is my affiliate link, I earn a small percentage from qualifying purchases) Do you want to learn functional analysis? In this video I talk about the book that I used to learn this amazing
From playlist Cool Math Stuff

Karlheinz Gröchenig: Gabor Analysis and its Mysteries (Lecture 2)
Due to technical problems the blackboard is not visible. The lecture was held within the framework of the Hausdorff Trimester Program Mathematics of Signal Processing. In Gabor analysis one studies the construction and properties of series expansions of functions with respect to a set of
From playlist HIM Lectures: Trimester Program "Mathematics of Signal Processing"

Functional Analysis Lecture 22 2014 04 15 L^p boundedness of Singular Integrals, ct’d.
(Continuing the proof) 1-atoms. Hormander condition. Control on atoms. Going for the weak-type estimate.
From playlist Course 9: Basic Functional and Harmonic Analysis

Karlheinz Gröchenig: Gabor Analysis and its Mysteries (Lecture 3)
Due to technical problems the blackboard is not visible. The lecture was held within the framework of the Hausdorff Trimester Program Mathematics of Signal Processing. In Gabor analysis one studies the construction and properties of series expansions of functions with respect to a set of
From playlist HIM Lectures: Trimester Program "Mathematics of Signal Processing"

Piotr Przytycki: Subgraphs of diameter 1 in graphs of girth 2
HYBRID EVENT Recorded during the meeting "Metric Graph Theory and Related Topics " the December 09, 2021 by the Centre International de Rencontres Mathématiques (Marseille, France) Filmmaker: Guillaume Hennenfent Find this video and other talks given by worldwide mathematicians on CIRM
From playlist Combinatorics

Karlheinz Gröchenig: Gabor Analysis and its Mysteries (Lecture 1)
The lecture was held within the framework of the Hausdorff Trimester Program Mathematics of Signal Processing. In Gabor analysis one studies the construction and properties of series expansions of functions with respect to a set of time-frequency shifts (phase space shifts) of a single fu
From playlist HIM Lectures: Trimester Program "Mathematics of Signal Processing"

OPTIMIZATION: Dimensions that maximize the volume of a box
► My Applications of Derivatives course: https://www.kristakingmath.com/applications-of-derivatives-course Optimization problems are an application of derivatives in calculus that allow us to find the local and global extrema of a function, including the local and global minima and the lo
From playlist Calculus I
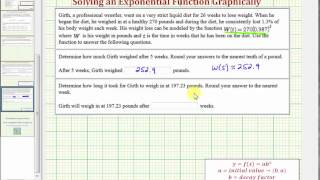
Ex: Solve an Exponential Decay Equation Graphically Using the TI84 (Application)
This video explains how to find exponential function values and solve an exponential equation graphically using the TI84.
From playlist Solving Applications of Exponential Growth and Decay

Calculus 1 Optimization Probelms b5p2
Calculus 1 Optimization Probelms b5p2 GoToMath.com
From playlist Calculus 1 GoToMath.com
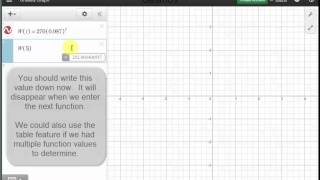
Ex: Solve an Exponential Decay Equation Graphically Using the Desmos (Application)
This video explains how to find exponential function values and solve an exponential equation graphically using the Desmos grapher.
From playlist Solving Applications of Exponential Growth and Decay

What are Meristematic Tissues? | Don't Memorise
Have you ever wondered how the roots and shoots of the plants grow so rapidly compared to the other plant parts? Well, that is because they have specialized tissues in these regions. Watch this video to know more about this tissue that gives the plants the ability to grow exceptionally wel
From playlist Tissues Class 09

Edward Ionides: Island filters for inference on metapopulation dynamics
Low-dimensional compartment models for biological systems can be fitted to time series data using Monte Carlo particle filter methods. As dimension increases, for example when analyzing a collection of spatially coupled populations, particle filter methods rapidly degenerate. We show that
From playlist Probability and Statistics

How to Evaluate a Multivariable Function Defined by an Integral
How to Evaluate a Multivariable Function Defined by an Integral If you enjoyed this video please consider liking, sharing, and subscribing. You can also help support my channel by becoming a member https://www.youtube.com/channel/UCr7lmzIk63PZnBw3bezl-Mg/join Thank you:)
From playlist Calculus 3

The Matching Problem in General Graphs is in Quasi-NC - Ola Svensson
Computer Science/Discrete Mathematics Seminar I Topic: The Matching Problem in General Graphs is in Quasi-NC Speaker: Ola Svensson Affiliation: École polytechnique fédérale de Lausanne Date: January 22, 2018 For more videos, please visit http://video.ias.edu
From playlist Mathematics

Common Linear Patterns Are Rare - Nina Kamčev
Computer Science/Discrete Mathematics Seminar I Topic: Common Linear Patterns Are Rare Speaker: Nina Kamčev Affiliation: University of Zagreb Date: April 03, 2023 Several classical results in Ramsey theory (including famous theorems of Schur, van der Waerden, Rado) deal with finding mon
From playlist Mathematics
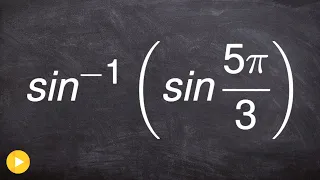
Evaluating the composition of Functions
👉 Learn how to evaluate an expression with the composition of a function and a function inverse. Just like every other mathematical operation, when given a composition of a trigonometric function and an inverse trigonometric function, you first evaluate the one inside the parenthesis. We
From playlist Evaluate a Composition of Inverse Trigonometric Functions

Jeff Erickson - Lecture 3 - Two-dimensional computational topology - 20/06/18
School on Low-Dimensional Geometry and Topology: Discrete and Algorithmic Aspects (http://geomschool2018.univ-mlv.fr/) Jeff Erickson (University of Illinois at Urbana-Champaign, USA) Two-dimensional computational topology - Lecture 3 Abstract: This series of lectures will describe recent
From playlist Jeff Erickson - School on Low-Dimensional Geometry and Topology: Discrete and Algorithmic Aspects
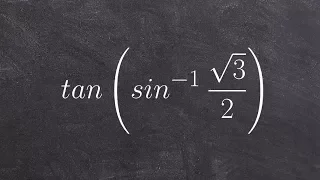
Evaluating the composition of Functions
👉 Learn how to evaluate an expression with the composition of a function and a function inverse. Just like every other mathematical operation, when given a composition of a trigonometric function and an inverse trigonometric function, you first evaluate the one inside the parenthesis. We
From playlist Evaluate a Composition of Inverse Trigonometric Functions

Evaluating the composition of Functions
👉 Learn how to evaluate an expression with the composition of a function and a function inverse. Just like every other mathematical operation, when given a composition of a trigonometric function and an inverse trigonometric function, you first evaluate the one inside the parenthesis. We
From playlist Evaluate a Composition of Inverse Trigonometric Functions